REV (667 points, 6 solves)

Here we explain the intended solution for the reversing challenge wreckme_again from our recent CTF.

Description

頑張って下さい (good luck)

Analysis

When initially opening this challenge with the decompiler of your choice you are greeted by some magic constants and many similar loops.

  v6 = (getline(&lineptr, &v55, stdin) - 0x5555555555555556LL) ^ 0xAAAAAAAAAAAAAAAALL;
  v7 = 0LL;
  v8 = v6;
  v9 = 0x2AAAAAAAAAAAAAAALL;
  do
  {
    v10 = v7;
    v11 = 2 * (v8 & v9);
    v12 = v8 ^ v9;
    v13 = v12 & ~v11;
    v8 = ~v13;
    v7 = ~v7;
    v9 = v11 & ~v12;
  }
  while ( v9 );
  v4 = v10 ^ v13;
  if ( (sub_2E50(0x2AAAAAAAAAAAAAABLL, v4) & 1) != 0 )
    goto LABEL_23;

The application to an integer value and subsequent usage suggests the constants to be part of some isomorphic or at least homomorphic mapping between possible integer representations. This construction with these constants indeed is used to switch between base 2 and base -2.

$v = \sum v_i * (-2)^i$

Thus the sign of each position flips between + and -. We can compare signed integer numbers represented in base 2 and base -2 using the following table

value	base 2	-8	4	-2	1	base -2
7	0111
6	0110
5	0101	0	1	0	1	0101
4	0100	0	1	0	0	0100
3	0011	0	1	1	1	0111
2	0010	0	1	1	0	0110
1	0001	0	0	0	1	0001
0	0000	0	0	0	0	0000
-1	1111	0	0	1	1	0011
-2	1110	0	0	1	0	0010
-3	1101	1	1	0	1	1101
-4	1100	1	1	0	0	1100
-5	1011	1	1	1	1	1111
-6	1010	1	1	1	0	1110
-7	1001	1	0	0	1	1001
-8	1000	1	0	0	0	1000
-9		1	0	1	1	1011
-10		1	0	1	0	1010

One can clearly see that for values between 5 and -8 there is a 1-to-1 mapping between both representations. Using a bit of python we can verify that 7 maps to -9 and 6 to -10. We conclude that both representations agree modulo 16.

With this knowledge we can deduce that the loop performs addition of v8 and v9 with the result computed in v4.

from numpy import (uint64 as u64)

def ton2(val):
    return (u64(val) - u64(0x5555555555555556)) ^ u64(0xaaaaaaaaaaaaaaaa)

Initial input processing

After checking some initial properties on the input (e.g., starts with “hxp{” and ends with “}”) there is a loop with some more intricate processing:

  v37 = 0x10D722ALL;
  do
  {
    v38 = sub_1B60(v37, 0x1A2A9FFDLL);
    sub_2130(v38, 0x605D6EE3LL);
    v39 = *v30;
    v40 = 0LL;
    v37 = v41;
    *(float *)v40.m128i_i32 = (float)(unsigned __int8)(*v30 & ~((unsigned __int8)*v30 >> 1)) + 0.5;
    v42 = ((((unsigned int)_mm_cvtsi128_si32(v40) >> 23) | 0xFE) + 1) & 0xE7;
    v43 = 0;
    do
    {
      v44 = v43;
      v45 = 2 * (v39 & v42);
      v46 = v39 ^ v42;
      v47 = v46 & ~v45;
      v39 = ~v47;
      v43 = ~v43;
      v42 = v45 & ~v46;
    }
    while ( v42 );
    *v30++ = v44 ^ v47;
  }
  while ( v37 != 1 );

First of all, let’s examine the induction variable.

  v37 = 0x10D722ALL;
  do
  {
    v38 = sub_1B60(v37, 0x1A2A9FFDLL);
    sub_2130(v38, 0x605D6EE3LL);
    v37 = v41;
  }
  while ( v37 != 1 );

IDA already warns us that v41 is potentially undefined. Therefore, we should take a close look at both these functions. As these function are full of vector intrinsics, I suggest to simply sample different inputs and outputs.

sub_1B60 does wide multiplication and sub_2130 appears to be a div-mod implementation. Luckily IDA is well equipped to handle these kind of functions, even in the free version. You can read up on it in Igor’s tip of the week #107. In short, you need to define a struct and then adjust the function signature.

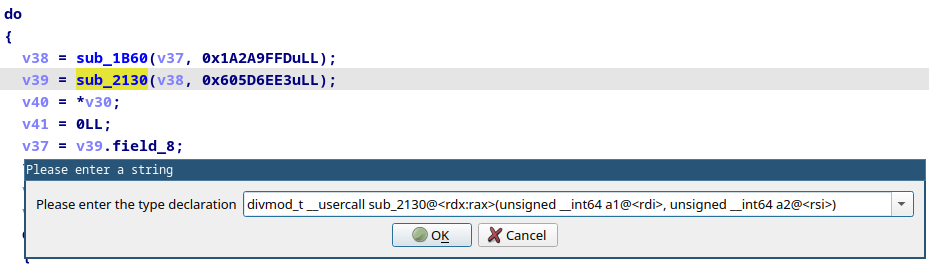
With our newfound knowledge we can rewrite the loop.

  v37 = 0xfd2dd6LL;
  do
  {
    v38 = v37 * 0x5d58aad;
    v37 = v38 % 0x204d199f;
  }
  while ( v37 != 1 );

This construction iterates over the subgroup generated by 0x5d58aad of the multiplicative group of $\mathbb{Z} / 541923743\mathbb{Z}$ starting from 0xfd2dd6.

From this information we can deduce the loop iteration count with a bit of sage:

import sys

if len(sys.argv) != 4:
    sys.exit(1)

init = int(sys.argv[1], 0)
mul = int(sys.argv[2], 0)
mod = int(sys.argv[3], 0)

G = Zmod(mod)

res = discrete_log(G(init), G(mul), G.unit_group().order())
loops = G.unit_group().order() - res
print(f"loop iterates {loops} times")

The rest of the loop looks a bit arcane but can also be rewritten to something sensible

if (inp[i] < 0)
    inp[i] += 0xa3;

Note that the input is treated as base -2, therefore this adjustment is applied to all digits and most special characters.

The final loop in main performs a memcmp, so sub_14c0 transforms the input in some way. Understanding this will yield the flag.

Input transformation

Initially, the transformation function is called like this:

transform(&inp[3], 0x40, 0, 27);

The function immediately recursively calls itself

void transform(uint8_t *data, int a, int b, int c) {
    int a_square = (a * a) % 0xa3;
    int a_cube = (a_square * a) % 0xa3;
    int tmp = abs(some_arr[a / 3]);
    transform(data, a_cube, b, c / 3);
    transform(data, a_cube, b + tmp, c / 3);
    transform(data, a_cube, b + tmp * 2, c / 3);
}

Later there is also some math modulo 0xa3 and two notable constants: 0x68 and 0x3a

From here one can either reverse the rest of this function or take educated guesses towards what is implemented here.

• 0x40 generates a multiplicative group of order 27 (is a 27th root of unity)

• 0x68 is 0x40^9 mod 0xa3

• 0x3a is 0x40^18 mod 0xa3

• 0x3a is 0x68^2 mod 0xa3

• The recursive call is done with a cubed number and a third of the number of elements

• Argument b is used to index into the data array

We can conclude that the function works on strides. Further, this construction somewhat resembles a fast Fourier transform (FFT). Reversing the rest of the function would indeed yield a butterfly construction for splitting the input 3-ways.

In sage, the final solve script looks as follows:

def fromn2(val):
  return ((val ^^ 0xaa) + 0x56) & 0xff

def ton2_and_adjust(val):
  v = ((val - 0x56) ^^ 0xaa) & 0xff
  if v >= 0x80:
    v = ((val + 0x100 - 0xa3 - 0x56) ^^ 0xaa) & 0xff
  return v

with open("wreckme_again", "rb") as f:
  f.seek(0x30c0)
  tvals = list(f.read(27))

G = Zmod(163)

# from base -2
tvals = [G(fromn2(tv)) for tv in tvals]

# build ft matrix
m = Matrix([[G(0x40) ^ (a * b) for b in range(27)] for a in range(27)])

# reposition strides
tmp = sum(((tvals[i::9] for i in [0,3,6,1,4,7,2,5,8])), [])

# inverse ft
sol = Matrix(tmp) * m.inverse()

sol = [ton2_and_adjust(s.lift()) for s in sol[0]]

print(bytes(sol).decode())