VolgaCTF 2016 Quals: crypto300 "XXY" writeup
In this task, one had to break an instance of the Goldreich-Goldwasser-Halevi lattice encryption scheme.
The task description reads:
I remember some of the AI engineers saying this was a very unusual cryptosystem. It was used to encrypt and transmit information of the enormous importance. Moreover, it seems there’s no need to share a key before the transmission.
We’ve found some kind of a key file, a ciphertext and the enciphering script itself. Is it possible to decrypt the data?
The script linked in the challenge description uses the following
sage function to encrypt a message:
def encrypt(plain_block, W, delta=151): n = W.ncols() m = vector([ord(ch) for ch in plain_block]) r = random_vector(ZZ, n, x=-delta+1, y=delta) e = m * W + r return e
In that snippet, $W$ is a unimodular square integer matrix
loaded from the key.public file.
That is, encryption essentially consists of the operation
\[ e \;=\; m\cdot W + r \]
where $r$ is a small random error vector and the message $m$ is suitably interpreted as an integer vector.
Now what seems to be required to obtain $m\cdot W$ (hence $m$) from
the disturbed vector $m\cdot W+r$ is solving the
closest vector problem (CVP)
in the lattice spanned by the columns of $W$. However, this seems to be,
to the best of public knowledge, quite hard in general, hence naïvely
throwing the given point into sage just heats your CPU for a long time.
However, as described by Phong Nguyen in 1999, the lattice used in the cryptosystem exhibits a rather large gap, that is, the shortest non-zero vector in the lattice is quite long (compared to the error vector $r$).
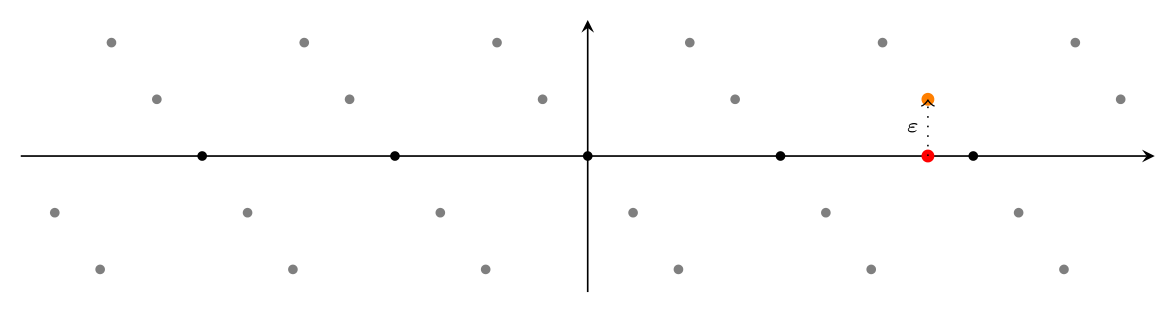
We shall therefore use the so-called embedding technique to solve the challenge. (A less visual description of this method can be found in section 18.3 of this book.) For illustration, we will pretend that our lattice is just $1$-dimensional, with the intuition easily carrying over to arbitrary dimensions. Suppose given the following CVP instance:

Here, lattice points are the black dots, and the point whose closest lattice point we are looking for is red. In the GGH setting, the red point would be $e=m\cdot W+r$ and the lattice would be spanned by $W$.
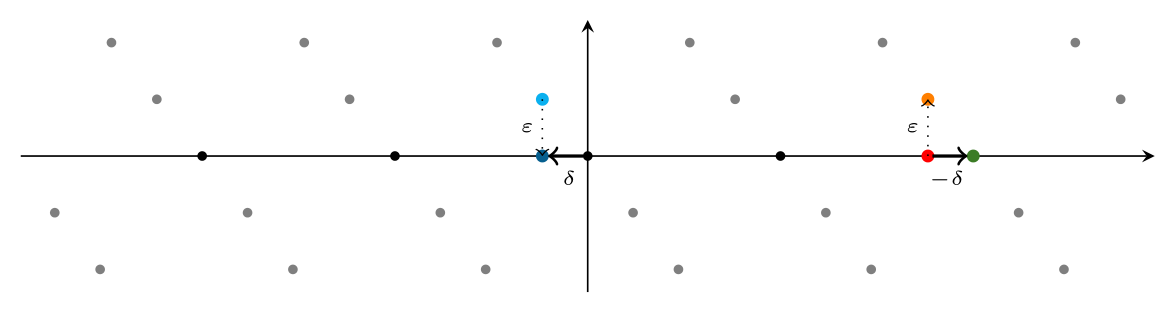
We can reduce this CVP instance to an instance of the shortest vector problem (SVP) by adding an additional dimension and basis vector to the lattice: The additional basis vector is given by shifting the given point $e$ a little bit $\varepsilon$ (for example $1$) along the new axis. In the following picture, the new basis vector is plotted orange, the lattice obtained this way is gray, and the original (embedded) lattice is still black.
If we now solve the SVP in that lattice and project the shortest vector back to the original lattice (essentially removing the extra coordinate added for the embedding) — let us call this vector $\delta$ —, then the error vector $r$ is just $\delta$, hence we can obtain $m$ as $(e-\delta)\cdot W^{-1}$. Again, a picture might help: The bright blue point is a solution to the SVP in the $2$-dimensional lattice; the dark blue point is its projection $\delta$ to the original lattice; and the green point on the right is the solution to the original CVP instance obtained by translating the given red point by $-\delta$.
Speaking code, this is surprisingly easy: Reusing the read_*
functions from crypt.py, the attack is fully implemented
in sage within a few lines:
#!/usr/bin/env sage
from crypt import read_mat, read_ciphertext
from sage.modules.free_module_integer import IntegerLattice
W = read_mat('key.public')
e = read_ciphertext('ciphertext')
B = W.stack(e).augment(vector([0] * W.ncols() + [1]))
d = IntegerLattice(B).shortest_vector()
print('d = {}'.format(d))
m = W.solve_left(e - d[:-1])
print('m = {}'.format(m))
print('\n --> {}'.format(''.join(map(chr, m))))
After only a few seconds, this prints the flag
$ ./pwn.sage d = (-4, -2, 4, -1, -2, -3, 2, -3, 3, 2, 0, 0, -2, -1, -4, 1, 2, -3, 2, 2, -2, -4, 0, 3, -4, -3, -1, -4, 3, 4, -4, -2, -4, -1, -2, -4, 2, -1, 1) m = (86, 111, 108, 103, 97, 67, 84, 70, 123, 71, 71, 72, 95, 117, 115, 101, 115, 95, 66, 97, 98, 97, 105, 95, 97, 110, 100, 95, 104, 97, 116, 101, 115, 95, 76, 76, 76, 125) --> VolgaCTF{GGH_uses_Babai_and_hates_LLL}
