VolgaCTF 2016 Quals: crypto600 "Five Blocks" writeup
This challenge exposed a chosen-plaintext oracle for a quite complicated homebrew block cipher, which one should use to decrypt a given ciphertext. Remarkably, we were the only team to solve this challenge during the CTF.
Task description:
The creators of the AI we’re so desperately looking for used the remote server to encrypt their data. It seems that this service merely encrypts the data we’re sending to it. We managed to find a possibly valuable piece of encrypted data along with the server’s script. Could you take a look and see if anything can be done?
nc five-blocks.2016.volgactf.ru 8888Hints
- What would you get if you’d encrypted four-block data of the form AABC, where A, B, C are 64-bit arbitrary blocks?
- Are the rounds of the second block cipher completely dependent or independent of each other? Or is the truth somewhere in the middle?
The block cipher consists of two individual ciphers, in the source called
bc1 and bc2, combined in a specific way.
It will turn out that bc1 is a very slightly modified variant of the
FEAL-4 cipher (which is vulnerable
to a differential chosen-plaintext attack), while the exact inner workings
of bc2 are largely irrelevant and only its outermost function must be
understood (admitting a
meet-in-the-middle attack).
Understanding/abusing the block cipher mode
The ciphers bc1 and bc2 are combined to the “full” encryption method via
the following functions from ciphers.py:
def pad(data, bs=8): r = len(data) % bs add_len = bs - r if r != 0 else bs add = '\x80' + '\x00'*(add_len-1) return data + add # ... def encrypt(self, data, iv): ciphertext = '' data = pad(data) C = iv for i in xrange(0, len(data), 8): A1 = self.bc1.encrypt_block(array.array('B', data[i:i+8])) A2 = self.bc2.decrypt_block(A1) ciphertext += block_xor(A2, C) C = A1 return ciphertext
It is quickly seen that this is a non-standard block mode, so I drew one of those fancy diagrams:
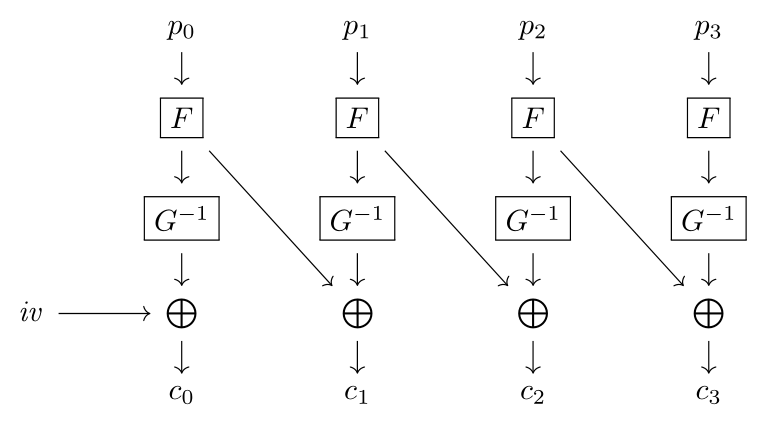
In that picture, $F$ and $G$ denote bc1 and bc2, respectively,
and the remaining symbols should be evident.
As suggested by the first hint given in the task description (which
came too late for us since we were already past that part when it was
published), an oracle for this construction can be made into an oracle
for bc1 only: Querying for an encryption of a plaintext of the form
$p_0\Vert p_0$, where $p_0$ is a single block, yields a ciphertext
$\mathit{iv}\Vert c_0\Vert c_1$, and the result of XORing all of its
blocks is evidently (check the diagram!) nothing but
\[
\mathit{iv}\oplus c_0\oplus c_1 \;=\; F(p_0) \text.
\]
Thus we have constructed an oracle for $F$, that is, bc1.
How to break bc1
At first glance, the code of bc1 is a standard Feistel network with a rather
easy round function. Staring at the code for another hour, I suddenly realized
it was in fact even more familiar than that:
bc1 is exactly the FEAL-4 cipher with the only modification that
the bit rotation in FEAL’s $G$ function rotates its output by
$4$ bits, not only $2$ as in the original FEAL.
Remembering the
differential chosen-plaintext attack on FEAL-4,
I quickly headed to the linked webpage (which is, by the way, excellent,
so I will not describe the attack here) to check whether it would still
apply to the modified version, and it does!
Only the differentials need to be changed, since the round function
now has the characteristic 0x80800000 -> 0x08000000 instead of
0x80800000 -> 0x02000000.
The author even provides a sample implementation of the attack in C.
Unfortunately (and recognizing/fixing this took another hour), the
code seems to assume that sizeof(unsigned long) == 4, hence breaks
completely on a modern x86_64 Linux system. Substituting all
occurrences of unsigned long by uint32_t (and,
optionally, s/unsigned long long/uint64_t/) at least makes the proof
of concept work for lucky choices of plaintexts and keys: As it turns
out, the method for breaking a single round key is complete but not
sound, that is, it may return a wrong key. If this happens, the
unmodified attack code can fail, since it simply takes the first
possible subkey and continues assuming it is correct.
We fixed this by always finding all potential subkeys for each round and
computing the remaining possible subkeys for each of them (this was a
dirty ad-hoc solution; much cleaner would’ve been a backtracking algorithm).
Moreover, since this made the search space a lot larger (but rendered the
algorithm complete!), we parallelized the attack such that it would run in
acceptable time on a somewhat powerful multi-core machine.
Of course, we had to remove all the code generating the chosen-plaintext
pairs, instead replacing them by pre-generated chosen-plaintext pairs from
a Python script querying the bc1 oracle described above.
After roughly ten minutes, the program presented us with 256 bc1 keys
— apparently all equivalent — that yield the same
bc1 instance as is running on the server. One of those keys is:
6c 21 3c 29 7b 03 fd 17 cb e3 b8 c8 bb d7 f1 03 d2 2a 2c 0e cc f5 48 dd
How to (not) obtain the flag without breaking bc2
Before investing time to put the attack on bc1 into practice,
we developed some approaches to take on the rest of the challenge
(few things are more frustrating than implementing tons of stuff to
not solve a task).
Being lazy, we tried to not have to analyze bc2 as well since it seemed
quite complicated at first sight.
One idea to solve the challenge without even looking at bc2, which
unfortunately did not work out due to the length of the flag but is
somewhat aesthetic, hence shall be presented, was the following:
If we knew some plaintext block of the (padded) flag, then we could
compute the previous plaintext block (hence, inductively, all previous
blocks) of the flag. This is done by solving the equation (look at the
diagram above again!)
\[
c_{i+1} \;=\; F(p_i)\oplus G^{-1}(F(p_{i+1}))
\]
for $p_i$, i.e.
\[
p_i \;=\; F^{-1}(c_{i+1}\oplus G^{-1}(F(p_{i+1}))) \text.
\]
Note that we can easily obtain $G^{-1}(F(p_{i+1}))$ using the oracle
by simply encrypting the single block $p_{i+1}$ and XORing out the
initialization vector. Computing $F^{-1}$ is — at this point —
trivial since we have a valid key for bc1.
Now if the last plaintext block of the flag consisted largely (say, except zero or one or two bytes) of padding, we could simply try all possible last blocks, each time trying the above attack to reconstruct the full “plaintext”, until it looks like a flag. We implemented this attack and let it run for all plaintext lengths congruent to $0$, $1$, or $2$ modulo the block size $8$, but got no flag this way.
As we shall see at the end, this is no surprise: The length of the flag is $\equiv7\pmod 8$, hence we would’ve had to guess 7 bytes correctly.
How to really break bc2
While an implementation of the idea above was running, the second hint
was published. Upon reading the hint, it was immediately clear to us
what bc2 was about: Reading the outermost function of bc2’s
encryption function
def encrypt_block(self, plaintext): (L0, R0) = struct.unpack('>II', plaintext) (L1, R1) = M(L0, R0, self.subkeys[0]) (L2, R2) = M(L1, R1, self.subkeys[1]) (L3, R3) = M(L2, R2, self.subkeys[2]) (CL, CR) = M(L3, R3, self.subkeys[3]) return struct.pack('>II', CL, CR)
clearly shows that it is susceptible to a meet-in-the-middle attack, allowing to brute-force two halves of the key independently. Moreover, the initialization function
def __init__(self, key): (k0, k1, k2, k3) = struct.unpack('>HHHH', key) K0 = pow(k0, 2) K1 = pow(k1, 2) K2 = pow(k2, 2) K3 = pow(k2, 2) self.subkeys = [K0, K1, K2, K3] print(self.subkeys)
contains a “typo” in the line K3 = pow(k2, 2): in fact k3 is
completely unused, making the search space small enough for the attack
to be highly practical. Hence, given a plaintext-ciphertext pair for bc2,
we may use the following routine to obtain the key in an acceptable time:
- For all $2^{16}$ possible subkeys $k_2$, invert the second
half of
encrypt_blockon the given ciphertext. Store the mapping of the resulting intermediate state to the subkey $k_2$ in a lookup table. - For all $2^{32}$ possible combinations of $k_0$ and $k_1$,
perform the first half of
encrypt_blockon the given plaintext. If the resulting intermediate state is in the lookup table built before, we have found a good tuple of subkeys.
bc2
can, again, easily be obtained using our local copy of bc1 and the oracle:
Having obtained some pair $(x,y)=(p, G^{-1}(F(p))$ from the oracle as above,
the pair $(y, F(x))$ is easily seen to be suitable.)Here’s code that performs this search:
#!/usr/bin/env python2
import struct, sys, os
from ciphers import inv_M, M, bc1, bc2
def enc1(subkey, plain):
L0, R0 = struct.unpack('>II', plain)
L1, R1 = M(L0, R0, subkey)
return struct.pack('>II', L1, R1)
def dec1(subkey, cipher):
L1, R1 = struct.unpack('>II', cipher)
L0, R0 = inv_M(L1, R1, subkey)
return struct.pack('>II', L0, R0)
key = '6c213c297b03fd17cbe3b8c8bbd7f103d22a2c0eccf548dd'.decode('hex')
# confusing names due to bc2's _de_cryption being used in bcs
plain = b'=\xfb\xc2\xc8Rq\x04k'
cipher = bc1(key).encrypt_block(b'01234567')
tab = {}
for key2 in range(0x10000):
k2 = key2 ** 2
tab[dec1(k2, dec1(k2, cipher))] = key2
print('table ready.')
threads, pids = 8, []
for i in range(threads):
pids.append(os.fork())
if pids[-1] == 0:
tid = i
break
else:
for pid in pids:
os.waitpid(pid, 0)
exit(0)
for key0 in range(tid, 0x10000, threads):
k0 = key0 ** 2
plain1 = enc1(k0, plain)
for key1 in range(0x10000):
k1 = key1 ** 2
plain2 = enc1(k1, plain1)
if plain2 in tab:
print('{:#x} {:#x} {:#x}'.format(key0, key1, tab[plain2]))
sys.stdout.write(' {:#06x}\r'.format(key0))
sys.stdout.flush()
Running this (heavily unoptimized) program takes about half an hour
and prints the (three quarters of) bc2 key:
0xe96a 0x5d75 0x631e
Flag!
We can now reassemble a working keys file that should be equivalent to
the server’s:
$ hexdump -C keys 00000000 6c 21 3c 29 7b 03 fd 17 cb e3 b8 c8 bb d7 f1 03 |l!<){...........| 00000010 d2 2a 2c 0e cc f5 48 dd e9 6a 5d 75 63 1e cc cc |.*,...H..j]uc...| 00000020
bc2’s initialization and can be chosen arbitrarily.)
>>> from ciphers import bcs >>> flag = open('flag.enc', 'rb').read() >>> keys = open('keys', 'rb').read() >>> print(bcs(keys[:6*4], keys[6*4:]).decrypt(flag[8:], flag[:8])) VolgaCTF{FEAL_is_weak_the_other_is_MITMable_and_the_mode_is_splittable}
And finally we see that the first approach to bypass bc2 was indeed
hopeless:
>>> len(bcs(keys[:6*4], keys[6*4:]).decrypt(flag[8:], flag[:8])) % 8 7
I wonder if the task author was aware of the attack and intentionally prevented it or if that was just by accident…
Update: Here’s what the author says:
The work on the task was done about a month before the game, but three weeks later I spent some time to analyse it and spotted that issue with known last block of the flag plaintext. But due to the chance the length was congruent 7 modulo 8. So, answering your semi-rhetorical question, I was aware of the attack and but it was prevented by accident :-) Well done!
