This challenge exposed a chosen-plaintext oracle for a quite complicated homebrew block cipher, which one should use to decrypt a given ciphertext. Remarkably, we were the only team to solve this challenge during the CTF.

Task description:

The creators of the AI we’re so desperately looking for used the remote server to encrypt their data. It seems that this service merely encrypts the data we’re sending to it. We managed to find a possibly valuable piece of encrypted data along with the server’s script. Could you take a look and see if anything can be done?

nc five-blocks.2016.volgactf.ru 8888

server ciphers data

Hints

1. What would you get if you’d encrypted four-block data of the form AABC, where A, B, C are 64-bit arbitrary blocks?
2. Are the rounds of the second block cipher completely dependent or independent of each other? Or is the truth somewhere in the middle?

The block cipher consists of two individual ciphers, in the source called bc1 and bc2, combined in a specific way.

It will turn out that bc1 is a very slightly modified variant of the FEAL-4 cipher (which is vulnerable to a differential chosen-plaintext attack), while the exact inner workings of bc2 are largely irrelevant and only its outermost function must be understood (admitting a meet-in-the-middle attack).

Understanding/abusing the block cipher mode

The ciphers bc1 and bc2 are combined to the “full” encryption method via the following functions from ciphers.py:

def pad(data, bs=8):
    r = len(data) % bs
    add_len = bs - r if r != 0 else bs
    add = '\x80' + '\x00'*(add_len-1)
    return data + add

# ...

def encrypt(self, data, iv):
    ciphertext = ''
    data = pad(data)
    C = iv
    for i in xrange(0, len(data), 8):
        A1 = self.bc1.encrypt_block(array.array('B', data[i:i+8]))
        A2 = self.bc2.decrypt_block(A1)
        ciphertext += block_xor(A2, C)
        C = A1
    return ciphertext

It is quickly seen that this is a non-standard block mode, so I drew one of those fancy diagrams:

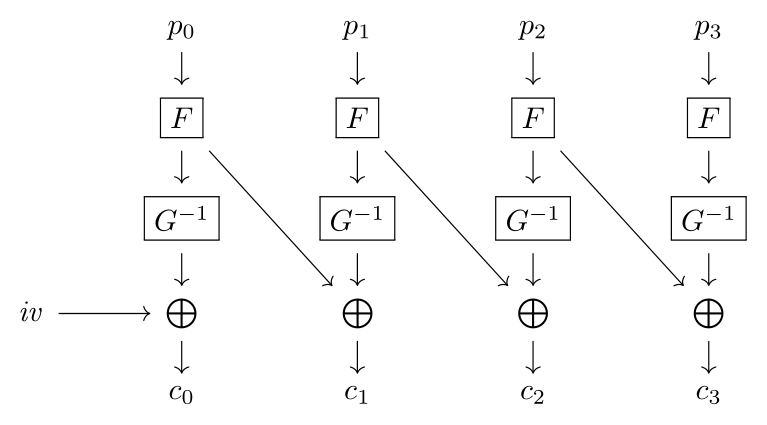
In that picture, $F$ and $G$ denote bc1 and bc2, respectively, and the remaining symbols should be evident.

As suggested by the first hint given in the task description (which came too late for us since we were already past that part when it was published), an oracle for this construction can be made into an oracle for bc1 only: Querying for an encryption of a plaintext of the form $p_0\Vert p_0$, where $p_0$ is a single block, yields a ciphertext $\mathit{iv}\Vert c_0\Vert c_1$, and the result of XORing all of its blocks is evidently (check the diagram!) nothing but \[ \mathit{iv}\oplus c_0\oplus c_1 \;=\; F(p_0) \text. \] Thus we have constructed an oracle for $F$, that is, bc1.

How to break bc1

At first glance, the code of bc1 is a standard Feistel network with a rather easy round function. Staring at the code for another hour, I suddenly realized it was in fact even more familiar than that: bc1 is exactly the FEAL-4 cipher with the only modification that the bit rotation in FEAL’s $G$ function rotates its output by $4$ bits, not only $2$ as in the original FEAL.

Remembering the differential chosen-plaintext attack on FEAL-4, I quickly headed to the linked webpage (which is, by the way, excellent, so I will not describe the attack here) to check whether it would still apply to the modified version, and it does! Only the differentials need to be changed, since the round function now has the characteristic 0x80800000 -> 0x08000000 instead of 0x80800000 -> 0x02000000.

The author even provides a sample implementation of the attack in C. Unfortunately (and recognizing/fixing this took another hour), the code seems to assume that sizeof(unsigned long) == 4, hence breaks completely on a modern x86_64 Linux system. Substituting all occurrences of unsigned long by uint32_t (and, optionally, s/unsigned long long/uint64_t/) at least makes the proof of concept work for lucky choices of plaintexts and keys: As it turns out, the method for breaking a single round key is complete but not sound, that is, it may return a wrong key. If this happens, the unmodified attack code can fail, since it simply takes the first possible subkey and continues assuming it is correct. We fixed this by always finding all potential subkeys for each round and computing the remaining possible subkeys for each of them (this was a dirty ad-hoc solution; much cleaner would’ve been a backtracking algorithm). Moreover, since this made the search space a lot larger (but rendered the algorithm complete!), we parallelized the attack such that it would run in acceptable time on a somewhat powerful multi-core machine. Of course, we had to remove all the code generating the chosen-plaintext pairs, instead replacing them by pre-generated chosen-plaintext pairs from a Python script querying the bc1 oracle described above. After roughly ten minutes, the program presented us with 256 bc1 keys — apparently all equivalent — that yield the same bc1 instance as is running on the server. One of those keys is:

6c 21 3c 29 7b 03 fd 17 cb e3 b8 c8 bb d7 f1 03 d2 2a 2c 0e cc f5 48 dd

How to (not) obtain the flag without breaking bc2

Before investing time to put the attack on bc1 into practice, we developed some approaches to take on the rest of the challenge (few things are more frustrating than implementing tons of stuff to not solve a task). Being lazy, we tried to not have to analyze bc2 as well since it seemed quite complicated at first sight. One idea to solve the challenge without even looking at bc2, which unfortunately did not work out due to the length of the flag but is somewhat aesthetic, hence shall be presented, was the following: If we knew some plaintext block of the (padded) flag, then we could compute the previous plaintext block (hence, inductively, all previous blocks) of the flag. This is done by solving the equation (look at the diagram above again!) \[ c_{i+1} \;=\; F(p_i)\oplus G^{-1}(F(p_{i+1})) \] for $p_i$, i.e. \[ p_i \;=\; F^{-1}(c_{i+1}\oplus G^{-1}(F(p_{i+1}))) \text. \] Note that we can easily obtain $G^{-1}(F(p_{i+1}))$ using the oracle by simply encrypting the single block $p_{i+1}$ and XORing out the initialization vector. Computing $F^{-1}$ is — at this point — trivial since we have a valid key for bc1.

Now if the last plaintext block of the flag consisted largely (say, except zero or one or two bytes) of padding, we could simply try all possible last blocks, each time trying the above attack to reconstruct the full “plaintext”, until it looks like a flag. We implemented this attack and let it run for all plaintext lengths congruent to $0$, $1$, or $2$ modulo the block size $8$, but got no flag this way.

As we shall see at the end, this is no surprise: The length of the flag is $\equiv7\pmod 8$, hence we would’ve had to guess 7 bytes correctly.

How to really break bc2

While an implementation of the idea above was running, the second hint was published. Upon reading the hint, it was immediately clear to us what bc2 was about: Reading the outermost function of bc2’s encryption function

def encrypt_block(self, plaintext):
    (L0, R0) = struct.unpack('>II', plaintext)
    (L1, R1) = M(L0, R0, self.subkeys[0])
    (L2, R2) = M(L1, R1, self.subkeys[1])
    (L3, R3) = M(L2, R2, self.subkeys[2])
    (CL, CR) = M(L3, R3, self.subkeys[3])
    return struct.pack('>II', CL, CR)

clearly shows that it is susceptible to a meet-in-the-middle attack, allowing to brute-force two halves of the key independently. Moreover, the initialization function

def __init__(self, key):
    (k0, k1, k2, k3) = struct.unpack('>HHHH', key)
    K0 = pow(k0, 2)
    K1 = pow(k1, 2)
    K2 = pow(k2, 2)
    K3 = pow(k2, 2)
    self.subkeys = [K0, K1, K2, K3]
    print(self.subkeys)

contains a “typo” in the line K3 = pow(k2, 2): in fact k3 is completely unused, making the search space small enough for the attack to be highly practical. Hence, given a plaintext-ciphertext pair for bc2, we may use the following routine to obtain the key in an acceptable time:

1. For all $2^{16}$ possible subkeys $k_2$, invert the second half of encrypt_block on the given ciphertext. Store the mapping of the resulting intermediate state to the subkey $k_2$ in a lookup table.
2. For all $2^{32}$ possible combinations of $k_0$ and $k_1$, perform the first half of encrypt_block on the given plaintext. If the resulting intermediate state is in the lookup table built before, we have found a good tuple of subkeys.

Here’s code that performs this search:

#!/usr/bin/env python2
import struct, sys, os
from ciphers import inv_M, M, bc1, bc2

def enc1(subkey, plain):
    L0, R0 = struct.unpack('>II', plain)
    L1, R1 = M(L0, R0, subkey)
    return struct.pack('>II', L1, R1)

def dec1(subkey, cipher):
    L1, R1 = struct.unpack('>II', cipher)
    L0, R0 = inv_M(L1, R1, subkey)
    return struct.pack('>II', L0, R0)

key = '6c213c297b03fd17cbe3b8c8bbd7f103d22a2c0eccf548dd'.decode('hex')

# confusing names due to bc2's _de_cryption being used in bcs
plain = b'=\xfb\xc2\xc8Rq\x04k'
cipher = bc1(key).encrypt_block(b'01234567')

tab = {}

for key2 in range(0x10000):
    k2 = key2 ** 2

    tab[dec1(k2, dec1(k2, cipher))] = key2

print('table ready.')

threads, pids = 8, []
for i in range(threads):
    pids.append(os.fork())
    if pids[-1] == 0:
        tid = i
        break
else:
    for pid in pids:
        os.waitpid(pid, 0)
    exit(0)

for key0 in range(tid, 0x10000, threads):
    k0 = key0 ** 2

    plain1 = enc1(k0, plain)

    for key1 in range(0x10000):
        k1 = key1 ** 2

        plain2 = enc1(k1, plain1)

        if plain2 in tab:
            print('{:#x} {:#x} {:#x}'.format(key0, key1, tab[plain2]))

    sys.stdout.write(' {:#06x}\r'.format(key0))
    sys.stdout.flush()

Running this (heavily unoptimized) program takes about half an hour and prints the (three quarters of) bc2 key:

0xe96a 0x5d75 0x631e

Flag!

We can now reassemble a working keys file that should be equivalent to the server’s:

$ hexdump -C keys
00000000  6c 21 3c 29 7b 03 fd 17  cb e3 b8 c8 bb d7 f1 03  |l!<){...........|
00000010  d2 2a 2c 0e cc f5 48 dd  e9 6a 5d 75 63 1e cc cc  |.*,...H..j]uc...|
00000020

>>> from ciphers import bcs
>>> flag = open('flag.enc', 'rb').read()
>>> keys = open('keys', 'rb').read()
>>> print(bcs(keys[:6*4], keys[6*4:]).decrypt(flag[8:], flag[:8]))
VolgaCTF{FEAL_is_weak_the_other_is_MITMable_and_the_mode_is_splittable}

And finally we see that the first approach to bypass bc2 was indeed hopeless:

>>> len(bcs(keys[:6*4], keys[6*4:]).decrypt(flag[8:], flag[:8])) % 8
7

I wonder if the task author was aware of the attack and intentionally prevented it or if that was just by accident…

Update: Here’s what the author says:

The work on the task was done about a month before the game, but three weeks later I spent some time to analyse it and spotted that issue with known last block of the flag plaintext. But due to the chance the length was congruent 7 modulo 8. So, answering your semi-rhetorical question, I was aware of the attack and but it was prevented by accident :-) Well done!