Google CTF 2017: reversing "moon"
This writeup explains how we solved a reversing task called moon during the
Google CTF last weekend. In summary, the task implements a password check
using OpenGL shaders.
Reconaissance
We’re given a Portable Executable (Download) for
x86-64 that was obviously compiled using MinGW (no
Rich header but the This program
cannot be run in DOS mode stub used typically used by MSVC – Borland prints a
different message):
00000000: 4d 5a 90 00 03 00 00 00 04 00 00 00 ff ff 00 00 |MZ..............|
00000010: b8 00 00 00 00 00 00 00 40 00 00 00 00 00 00 00 |........@.......|
00000020: 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 |................|
00000030: 00 00 00 00 00 00 00 00 00 00 00 00 80 00 00 00 |................|
00000040: 0e 1f ba 0e 00 b4 09 cd 21 b8 01 4c cd 21 54 68 |........!..L.!Th|
00000050: 69 73 20 70 72 6f 67 72 61 6d 20 63 61 6e 6e 6f |is program canno|
00000060: 74 20 62 65 20 72 75 6e 20 69 6e 20 44 4f 53 20 |t be run in DOS |
00000070: 6d 6f 64 65 2e 0d 0d 0a 24 00 00 00 00 00 00 00 |mode....$.......|
00000080: 50 45 00 00 64 86 09 00 00 00 00 00 00 00 00 00 |PE..d...........|
In general, Portable Executables tend to come together with a lot of statically
linked-in library code, which we usually are not interested in during reversing.
As such, the most convenient way of determining the main function in Windows
binaries that occur during CTFs is usually just quickly searching for suspicious
strings such as “Wrong”, “Congratz”, “flag”, or even the program name. Moreover,
as compilers are quite deterministic, all non-library strings will be placed
close to each other. And indeed, using the hacker tool strings once more we
find:
➜ moon strings moon.exe| grep -iC8 moon
%.8x
glGetShaderiv:
glCompileShader:
GL_TIMEOUT_EXPIRED or GL_WAIT_FAILED
vert_xyz
vert_uv
NopeGood
SDL_Init: %s
Moon
gl3wInit()
OpenGL 4.3 not supported
basic_string::append
timeout error
Bye bye...
30c7ead97107775969be4ba00cf5578f1048ab1375113631dbb6871dbe35162b1c62e982eb6a7512f3274743fb2e55c818912779ef7a34169a838666ff3994bb4d3c6e14ba2d732f14414f2c1cb5d3844935aebbbe3fb206343a004e18a092daba02e3c0969871548ed2c372eb68d1af41152cb3b61f300e3c1a8246108010d282e16df8ae7bff6cb6314d4ad38b5f9779ef23208efe3e1b699700429eae1fa93c036e5dcbe87d32be1ecfac2452ddfdc704a00ea24fbc2161b7824a968e9da1db756712be3e7b3d3420c8f33c37dba42072a941d799ba2eebbf86191cb59aa49a80ebe0b61a79741888cb62341259f62848aad44df2b809383e09437928980f
?UUU?
glActiveProgramEXT
Hmm … We can spot “Nope” and “Good”, which probably indicate whether we were
successful, a “Bye bye” message that apparently is printed when the program is
closed and a high entropy hexadecimal string that already should catch our
attention. Additionally, we can see several instances of the letters gl, which
hint towards OpenGL being used in the program. Let’s fire up IDA and see what is
going on inside the binary!
Digging Deeper
Searching backwards from the long hexstring in IDA, we find a function that performs all kinds of interesting static initializations. After doing some cleanup und some renaming, the Hex-Rays output looks as follows:
__int64 init_global_vars()
{
some_byte_foo_ptr = (__int64)&some_byte_foo_dat;
new_basic_string((_BYTE **)&some_byte_foo_ptr, byte_49A010, aVersion430InVec3Ve);
sub_411C40();
shader_one_ptr = (__int64)&shader_one_dat;
new_basic_string((_BYTE **)&shader_one_ptr, &aVersion430InVec3Ve[315], &aVersion430InVec3Ve[491]);
sub_411C40();
shader_two_ptr = (__int64)&shader_two_dat;
new_basic_string((_BYTE **)&shader_two_ptr, aVersion430InVec3Ve, &aVersion430InVec3Ve[315]);
sub_411C40();
letters_png_ptr = (__int64)&letters_png_dat;
new_basic_string((_BYTE **)&letters_png_ptr, &unk_49C23A, &off_49CBD0);
sub_411C40();
qword_4CA088 = 0i64;
qword_4CA080 = &byte_4CA090;
byte_4CA090 = 0;
sub_411C40();
long_hexstring_ptr = &long_hexstring_dat;
new_basic_string(
(_BYTE **)&long_hexstring_ptr,
"30c7ead97107775969be4ba00cf5578f1048ab1375113631dbb6871dbe35162b1c62e982eb6a7512f3274743fb2e55c818912779ef7a34169a83"
"8666ff3994bb4d3c6e14ba2d732f14414f2c1cb5d3844935aebbbe3fb206343a004e18a092daba02e3c0969871548ed2c372eb68d1af41152cb3"
"b61f300e3c1a8246108010d282e16df8ae7bff6cb6314d4ad38b5f9779ef23208efe3e1b699700429eae1fa93c036e5dcbe87d32be1ecfac2452"
"ddfdc704a00ea24fbc2161b7824a968e9da1db756712be3e7b3d3420c8f33c37dba42072a941d799ba2eebbf86191cb59aa49a80ebe0b61a7974"
"1888cb62341259f62848aad44df2b809383e09437928980f",
"");
return sub_411C40();
}
At the bottom, we see the contents of long_hexstring being assigned to a
dynamically allocated std::string. In total new_basic_string (which we named
according to the error messages found in this binary function) is called four
times with four different arguments:
- Some non-printable gibberish at address
0x49A010 A string representing a program written in a C-like language:
#version 430 in vec3 vert_xyz; in vec2 vert_uv; out vec2 frag_uv; void main() { frag_uv = vert_uv; // Rescale the scene so it's in pixels. gl_Position = vec4( (vert_xyz.x / 1280.0) * 2.0 - 1.0, -((vert_xyz.y / 720.0) * 2.0 - 1.0), vert_xyz.z / 1024.0, 1.0 );Another program:
#version 430 in vec2 frag_uv; out vec4 frag_colour; uniform sampler2D tex; void main() { frag_colour = vec4(1.0, 1.0, 1.0, 1.0) * texture(tex, frag_uv);Something that starts with a PNG header at address
0x49C23Awhich, dumped usingbinwalk, looks like the charset used by the program:
Okay, we can clearly understand why the program needs the PNG, but what are those mysterious C-like snippets about? A brief query to our search engine of choice tells us that we are dealing with OpenGL Shading Language (abbreviated GLSL). In summary, GLSL allows for embedding shaders into a program that get compiled to ARB Assembly Language which then in turn can be uploaded to the graphics hardware for further processing. Nevertheless, the two snippets we found above are totally boring and don’t do anything that is of interest for us. Let’s try to find out what that unreadable gibberish (no. 1 from the list above) was.
Looking at the locations from where some_byte_foo_ptr is accessed, we can spot
a simple string scrambling function (at 0x401a30):
if ( some_byte_foo_ptr != qword_4CA128 + some_byte_foo_ptr )
{
v2 = 1i64;
v3 = (_BYTE *)(some_byte_foo_ptr + 1);
v4 = 0i64;
v5 = -561040962;
v6 = *(_BYTE *)some_byte_foo_ptr ^ 0xBE;
while ( 1 )
{
*((_BYTE *)v0 + v4) = v6;
v17 = v2;
*((_BYTE *)Memory + v2) = 0;
if ( v3 == (_BYTE *)v1 )
break;
v7 = v5;
v8 = v5;
v9 = __ROL4__(v5, 3);
v4 = v17;
v10 = (v8 >> 21) ^ (v7 << 8);
v11 = 15i64;
v5 = v10 + v9 - 0x6837E5D9;
v0 = (__int64 *)Memory;
v2 = v17 + 1;
v6 = *v3 ^ v5;
if ( Memory != &v18 )
v11 = v18;
++v3;
if ( v2 > v11 )
{
sub_4870A0(&Memory, v17, 0i64, 0i64);
v0 = (__int64 *)Memory;
}
}
}
At this point, we anticipated that unscrambling the string was not the main
point of the challenge, and therefore we just decided to use
x64dbg to dump the unscrambled data. This can easily
be done by setting a breakpoint to 0x401B30 (which is directly after the loop)
and patching up 0x401aa0 (containing a mov r14d, 0x0F) to actually
unscramble more than just the first 15 bytes of the data. Afterwards, the
data can be dumped conveniently from memory referenced by location rsp+0x60.
Reversing The Core
After fixing indentation and line breaks we get something that arouses interest immediately:
#version 430
layout(local_size_x=8,local_size_y=8)in;
layout(std430,binding=0) buffer shaderExchangeProtocol{
uint state[64];
uint hash[64];
uint password[32];
};
vec3 calc(uint p) {
float r = radians(p);
float c = cos(r);
float s = sin(r);
mat3 m = mat3(c, -s, 0.0, s, c, 0.0, 0.0, 0.0, 1.0);
vec3 pt = vec3(1024.0, 0.0, 0.0);
vec3 res = m*pt;
res += vec3(2048.0, 2048.0, 0.0);
return res;
}
uint extend(uint e) {
uint i;
uint r = e ^ 0x5f208c26;
for (i = 15; i < 31; i += 3){
uint f = e << i;
r ^= f;
}
return r;
}
uint hash_alpha(uint p) {
vec3 res=calc(p);
return extend(uint(res[0]));
}
uint hash_beta(uint p) {
vec3 res=calc(p);
return extend(uint(res[1]));
}
void main(){
uint idx = gl_GlobalInvocationID.x + gl_GlobalInvocationID.y * 8;
uint final;
if (state[idx] != 1){
return;
}
if ((idx & 1) == 0){
final = hash_alpha(password[idx/2]);
}else{
final = hash_beta(password[idx/2]);
}
uint i;
for (i=0; i < 32; i += 6){
final ^= idx << i;
}
uint h = 0x5a;
for (i = 0; i < 32; i++){
uint p = password[i];
uint r = (i * 3) & 7;
p = (p << r) | (p >> (8 - r));
p &= 0xff;
h ^= p;
}
final ^= (h | (h << 8) | (h << 16) | (h << 24));
hash[idx] = final;
state[idx] = 2;
memoryBarrierShared();
}
What we can see above is a simple transformation of data risiding in an array
password. Note that despite the term hash being used by the challenge author
(we did not rename anything in the code above), the steps performed by the
algorithm are actually reversible. Let’s discuss the above shader a bit more
in-depth. The first thing to understand is probably IO behaviour:
layout(std430,binding=0) buffer shaderExchangeProtocol{
uint state[64];
uint hash[64];
uint password[32];
};
This defines three arrays state, hash, and password. As we can infer from
the main function, password is used for reading in data, hash is used for
storing the result of the computation, and state is (presumably) used to
signal whether a certain worker thread on the GPU already has finished the
calculation …
… which brings us to how processing on the GPU is done in general. The line
uint idx = gl_GlobalInvocationID.x + gl_GlobalInvocationID.y * 8;
and the fact that the hash array stores 64 results tells us that our GPU cores
are organized in a 8 x 8 grid. The runtime assigns a (x, y) position in that
grid to each of the cores. From this grid position, the code can then calculate a
unique id, resulting in the transformation being invoked in parallel for
different input characters.
Let’s look at the actual computation steps that are eventually performed. The
first one is calc, which involves some linear algebra magic.
vec3 calc(uint p) {
float r = radians(p);
float c = cos(r);
float s = sin(r);
mat3 m = mat3(c, -s, 0.0, s, c, 0.0, 0.0, 0.0, 1.0);
vec3 pt = vec3(1024.0, 0.0, 0.0);
vec3 res = m*pt;
res += vec3(2048.0, 2048.0, 0.0);
return res;
}
Even though this looks intimidating, the operation is quite simple: What we can
see here is that p is used to construct a Rotation
Matrix by p degrees in the
$(x, y)$ plane which gets applied to the vector $(1024, 0, 0)$ (the third
coordinate is left untouched). Afterwards, the result is translated (shifted) in
the $(x, y)$ plane by $(2048, 2048)$. With this knowledge, it becomes clear that
(assuming user input within ASCII range $(0, 255)$) this operation can easily be
inverted. In fact, if the python version of calc looks like follows:
def calc(p):
r = math.radians(ord(p))
c = math.cos(r)
s = math.sin(r)
m = [[ c, -s, 0.0],
[ s, c, 0.0],
[0.0, 0.0, 1.0]]
pt = [ 1024.0, 0.0, 0.0 ]
res = np.dot(m, pt)
res += [2048.0, 2048.0, 0.0]
return res
then the reverse operation rev_calc can be implemented by simply un-doing the
translation and then calculating the angle of the resulting vector and the
vector pointing into direction $(1024, 0, 0)$:
import math
import numpy as np
def unit_vector(vector):
return vector / np.linalg.norm(vector)
def angle_between(v1, v2):
v1_u = unit_vector(v1)
v2_u = unit_vector(v2)
return np.arccos(np.clip(np.dot(v1_u, v2_u), -1.0, 1.0))
def rev_calc(res):
res = np.subtract(res, [2048.0, 2048.0, 0.0])
p = angle_between(res, [1024.0, 0.0, 0.0])
return chr(int(math.degrees(p)))
The second computation step uses more traditional fixed length integer arithmetic
uint extend(uint e) {
uint i;
uint r = e ^ 0x5f208c26;
for (i = 15; i < 31; i += 3){
uint f = e << i;
r ^= f;
}
return r;
}
Looking carefully at this function, we can see that every third of the bits 0 to
14 is xored into the upper half of r. Since r is the input xored by a fixed
constant, the lowest 15 bits remain untouched and the operation becomes
trivially invertible:
def extend(e):
r = e ^ 0x5f208c26
for i in range(15, 31, 3):
r ^= (e << i) & 0xffffffff
return r & 0xffffffff
def rev_extend(r):
l = ((r ^ 0x5f208c26) & ((1 << 15) - 1))
for i in range(15, 31, 3):
r ^= (l << i) & 0xffffffff
return (r ^ 0x5f208c26) & 0xffffffff
Let’s look at the main function of the shader again:
void main(){
uint idx = gl_GlobalInvocationID.x + gl_GlobalInvocationID.y * 8;
uint final;
if (state[idx] != 1){
return;
}
if ((idx & 1) == 0){
final = hash_alpha(password[idx/2]);
}else{
final = hash_beta(password[idx/2]);
}
uint i;
for (i=0; i < 32; i += 6){
final ^= idx << i;
}
uint h = 0x5a;
for (i = 0; i < 32; i++){
uint p = password[i];
uint r = (i * 3) & 7;
p = (p << r) | (p >> (8 - r));
p &= 0xff;
h ^= p;
}
final ^= (h | (h << 8) | (h << 16) | (h << 24));
hash[idx] = final;
state[idx] = 2;
memoryBarrierShared();
}
As extend and calc are used by hash_alpha and hash_beta, we are now
fully able to invert the first part of the algorithm. Nice!
What about the remaining steps?
So far, the transformation was performed for each character independently from each other (observe how password is just accessed by means of the global id). To stop simple character wise brute force, this obviously has to change; which is what the second part of the transformation deals with:
for (i=0; i < 32; i += 6){
final ^= idx << i;
}
uint h = 0x5a;
for (i = 0; i < 32; i++){
uint p = password[i];
uint r = (i * 3) & 7;
p = (p << r) | (p >> (8 - r));
p &= 0xff;
h ^= p;
}
final ^= (h | (h << 8) | (h << 16) | (h << 24));
The first for loop simply xors the global id idx to the result at several
postions. The more devastating part is the second loop: All characters of the
password are accumulated into one byte value by combining a bitwise rotate with
a multiplication by $3$. The result is then promoted to a 32 bit value by simply
duplicating the lowest byte and then xoring it to the final hash value. We don’t
know the value of h and therefore cannot reconstruct final from before the
final xor. Damn. Or can we?
Thinking about this a second we came to the conclusion that this it can be broken by performing a known plaintext attack on the target value the thread with idx 0. But, wait, what are our target values? Remember the long hexstring? Let’s get back to the binary a second time!
This is the main function of the binary after cleaning it up and teaching IDA
about SDL headers:
SDL_StartTextInput();
do
{
while ( SDL_PollEvent(&event) )
{
evt_type = event.type;
if ( event.type == SDL_QUIT )
goto LABEL_34;
if ( event.type - 768 > 1 )
goto LABEL_15;
if ( event.window.event == SDL_PEEKEVENT )
{
if ( event.window.data2 == 27 )
{
LABEL_34:
v21 = v30;
goto LABEL_35;
}
if ( (event.window.data2 == 0x400000BB || event.window.data2 == 8) && qword_4CA088 )
{
sub_486E60((__int64)&qword_4CA080, qword_4CA088 - 1, 1i64);
evt_type = event.type;
cmp_flag = 0;
LABEL_15:
if ( evt_type == SDL_TEXTINPUT && strlen(event.edit.text) == 1 )
{
if ( (unsigned __int64)qword_4CA088 <= 0x1F )
{
string_append((__int64)&qword_4CA080, &event.jhat.hat, 1ui64);
if ( qword_4CA088 == 32 )
goto LABEL_27;
LABEL_19:
cmp_flag = 0;
}
else
{
if ( qword_4CA088 != 32 )
goto LABEL_19;
LABEL_27:
v17 = (__int128 *)v42;
Size = 0i64;
v35 = 0;
Memory = &v35;
if ( (unsigned __int8)do_check(qword_4CA080, (unsigned int *)v42) )
{
do
{
v18 = *(_DWORD *)v17;
*(_QWORD *)Dest = 0i64;
v32 = 0;
sprintf_0(Dest, "%.8x", v18);
v19 = &Dest[strlen(Dest)];
if ( v19 - Dest > 0x7FFFFFFFFFFFFFFFi64 - Size )
sub_4921C0("basic_string::append");
string_append((__int64)&Memory, Dest, v19 - Dest);
v17 = (__int128 *)((char *)v17 + 4);
}
while ( &v43 != v17 );
v20 = (char *)Memory;
if ( Size != long_hexstring_data || Size && memcmp(Memory, long_hexstring_ptr, Size) )
cmp_flag = 1;
else
cmp_flag = 2;
}
else
{
v25 = __iob_func();
sub_41E440(&v25[2], "timeout error\n", v26);
v20 = (char *)Memory;
}
if ( v20 != &v35 )
j_free(v20);
}
}
}
}
}
v21 = 0;
LABEL_35:
v22 = SDL_GetTicks();
*(float *)&v23 = (float)((float)v22 / 1000.0) - *(float *)&dword_4CA044;
*(float *)&dword_4CA044 = (float)v22 / 1000.0;
dword_4CA040 = v23;
SDL_GL_MakeCurrent(v27, v28);
glUseProgram((unsigned int)dword_4CA0A4);
sub_402660((float *)&v36);
glUseProgram(0i64);
SDL_GL_SwapWindow(v27);
}
while ( !v21 );
puts("Bye bye...");
The long_hexstring_ptr is used here in a memcmp. The rest of the code is
boilerplate to read in user input, store it at 0x4ca080 and then throw it into
do_check. This function, unsurprisingly, invokes the secreet shader with the
input the user entered (renaming the global function names based on string
analysis where the pointer values are actually obtained from GetProcAddress):
glUseProgram((unsigned int)flagCheckProgram);
if ( !(unsigned char)glIsBuffer((unsigned int)dword_4CA0A0) )
{
memset(Dst, 0, 0x280ui64);
glGenBUffers(1i64, &dword_4CA0A0);
glBindBufferBase(37074i64, 0i64, (unsigned int)dword_4CA0A0);
glBindBuffer(37074i64, (unsigned int)dword_4CA0A0);
glBufferData(37074i64, 640i64, Dst, 35048i64);
}
// ...
glDispatchCompute(8i64, 8i64, 1i64);
LODWORD(v21) = glFenceSync(37143i64, 0i64);
v22 = v21;
if ( (glClientWaitSync(v21, 1i64, 1000000000i64) - 37147) & 0xFFFFFFFD )
// ...
Alright, no surprises here, the long_hexstring_ptr is the result of the
computation of our 8 x 8 gpu thread grid. Let’s finish this …
Remember, we perform a known-plaintext attack on the value of h in the
shader’s main function that is xored to the final variable in the last step.
We assume that the password starts with a “C” (for CTF{}, yay flag format) and
do the following in our python script (remember, idx 0 skips the second last xor
loop):
import math, struct, binascii
import numpy as np
dat = binascii.unhexlify(open('magic', 'r').read().strip())
u = lambda x: struct.unpack(">I", x)[0]
grid = [ [ u(dat[j * 32 + i * 4:][:4]) for i in range(8) ] for j in range(8) ]
print(hex(extend(int(calc('C')[0] + 0)) ^ grid[0][0]))
➜ moon ./pwn.py
0x6f6f6f6f
Success! The fact that we can see four duplicated byte values tells us that for the correct password
uint h = 0x5a;
for (i = 0; i < 32; i++){
uint p = password[i];
uint r = (i * 3) & 7;
p = (p << r) | (p >> (8 - r));
p &= 0xff;
h ^= p;
}
ends up with h = 0x6f.
Success
This is the final solution script (with magic being just the
long hex string that we obtained running strings):
#!/usr/bin/env python3
import math, struct, binascii
import numpy as np
dat = binascii.unhexlify(open('magic', 'r').read().strip())
u = lambda x: struct.unpack(">I", x)[0]
grid = [ [ u(dat[j * 32 + i * 4:][:4]) for i in range(8) ] for j in range(8) ]
tgt = grid[0][0]
def unit_vector(vector):
return vector / np.linalg.norm(vector)
def angle_between(v1, v2):
v1_u = unit_vector(v1)
v2_u = unit_vector(v2)
return np.arccos(np.clip(np.dot(v1_u, v2_u), -1.0, 1.0))
def extend(e):
r = e ^ 0x5f208c26
for i in range(15, 31, 3):
r ^= (e << i) & 0xffffffff
return r & 0xffffffff
def rev_extend(r):
l = ((r ^ 0x5f208c26) & ((1 << 15) - 1))
for i in range(15, 31, 3):
r ^= (l << i) & 0xffffffff
return (r ^ 0x5f208c26) & 0xffffffff
def calc(p):
r = math.radians(ord(p))
c = math.cos(r)
s = math.sin(r)
m = [[ c, -s, 0.0],
[ s, c, 0.0],
[0.0, 0.0, 1.0]]
pt = [ 1024.0, 0.0, 0.0 ]
res = np.dot(m, pt)
res += [2048.0, 2048.0, 0.0]
return res
def rev_calc(res):
res = np.subtract(res, [2048.0, 2048.0, 0.0])
p = angle_between(res, [1024.0, 0.0, 0.0])
return chr(int(math.degrees(p)))
def second(x, y):
final = extend(int(calc('C')[0] + 0)) ^ grid[0][0]
idx = x + y * 8
tgt = grid[y][x] ^ final
for i in range(0, 32, 6):
tgt ^= (idx << i) & 0xffffffff
return tgt
print(hex(extend(int(calc('C')[0] + 0)) ^ grid[0][0]))
y = 0
x = 0
for y in range(8):
for x in range(0, 8, 2):
tmp = [ rev_extend(second(x, y)), rev_extend(second(x + 1, y)), 0.0 ]
z = rev_calc([ rev_extend(second(x, y)), rev_extend(second(x + 1, y)), 0.0 ])
print(z, end = '')
print('')
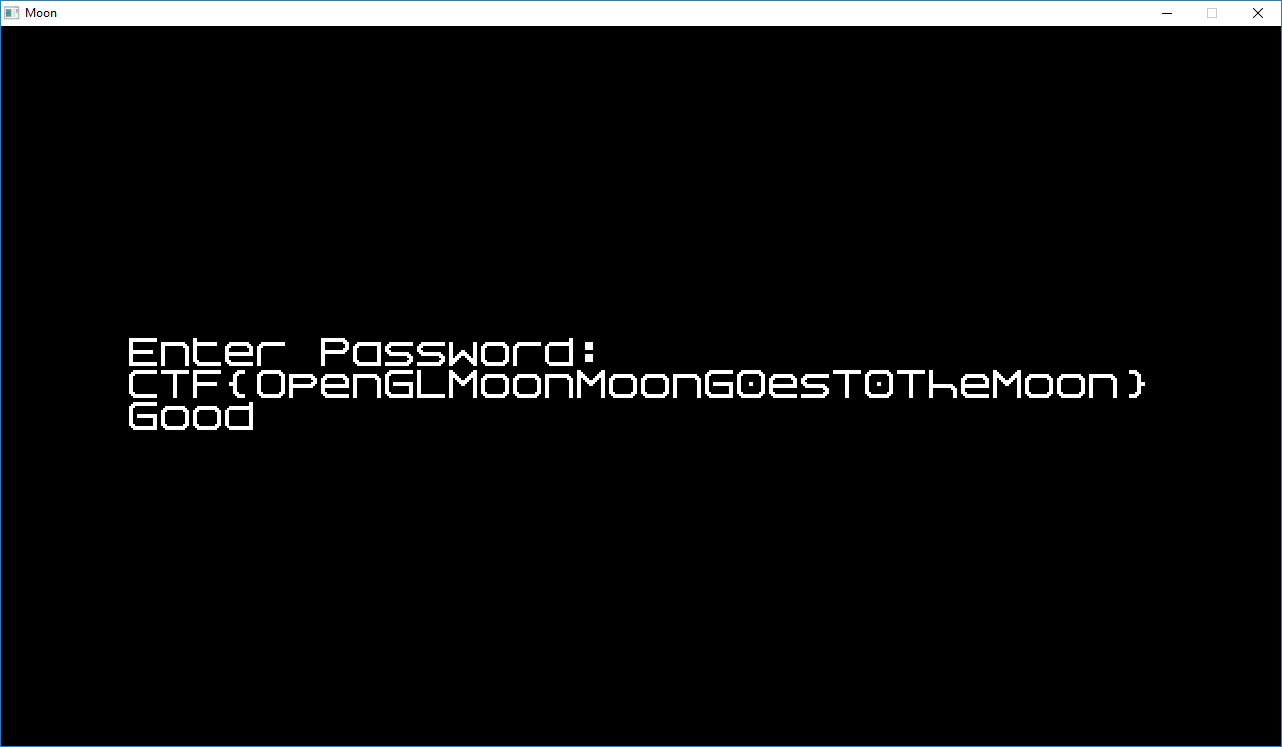
Executing the script gives as (almost) the flag:
➜ moon ./pwn.py
0x6f6f6f6f
CTF{OpenGLMoonMoonG0erT0TheMoon}
Which, after some guessing gave us the correct flag: