hxp CTF 2022: the_swirl writeup
Here we explain the intended solution for the cryptography+reversing challenge the_swirl from our recent CTF, which no team managed to solve during the competition.
The goal of the challenge was to break a Ring‑LWE key-encapsulation mechanism (KEM) by exploiting leakage from a botched NTT‑based implementation of the multiplication in the underlying polynomial ring $R = \mathbb F_q[X]/(X^{256}+1)$, where $q=11777$.
The task consisted of a Python script, eerily similar to the source code of the significantly easier whistler challenge, and a compiled shared library which contains an AVX2‑vectorized implementation of multiplication in $R$. The server starts by printing a public key and an encryption of the flag, then enters an infinite loop of responding to a simple ping‑pong protocol which involves completing a decapsulation and responding with an encrypted message under the resulting key.
First, how do the obvious ideas fail?
- Trying the same approach as for "whistler" cannot work since the KEM scheme now includes a version of the Fujisaki‑Okamoto transform (FO): Basically, this means all client‑side randomness is generated from a single random seed, which is revealed to the server immediately following the key exchange. The server then re‑runs the encapsulation performed by the client and replaces the shared secret by a random bit string if the result does not match the actual data sent by the client, as to prevent the kind of leakage that lies at the heart of solving "whistler": Any attempt at deviating from the honest encapsulation routine causes the same kind of failure, irrespective of the reason.
-
Brute‑force solving the underlying lattice problem
might be barely feasible in principle using
absolutely massive computational resources,
but certainly not within the timeframe of the CTF.
The very useful
lattice estimator
predicts a cost of $2^{74.2}$ operations to recover
the secret key using the standard uSVP attack:
In true 2023 fashion, we may then ask ChatGPT to interpret this result for us:

Figuring out what's going on
Playing around with the code for a bit
should make you notice fairly quickly that
the new mul() function gives
wrong results for some inputs.
To find out why and how, we have to dig
into the code, most of which — to everyone's
great dismay — looks somewhat like this:
// ...
10ee: c5 b5 e4 e6 vpmulhuw ymm4,ymm9,ymm6
10f2: c5 b5 d5 f6 vpmullw ymm6,ymm9,ymm6
10f6: c4 c1 4d d5 f6 vpmullw ymm6,ymm6,ymm14
10fb: c4 c1 4d e4 f7 vpmulhuw ymm6,ymm6,ymm15
1100: c5 dd f9 e6 vpsubw ymm4,ymm4,ymm6
1104: c4 c1 5d fd f7 vpaddw ymm6,ymm4,ymm15
1109: c4 e2 5d 3a e6 vpminuw ymm4,ymm4,ymm6
110e: c5 fd f9 f4 vpsubw ymm6,ymm0,ymm4
1112: c5 fd fd c4 vpaddw ymm0,ymm0,ymm4
1116: c4 c1 4d fd e7 vpaddw ymm4,ymm6,ymm15
111b: c4 e2 5d 3a e6 vpminuw ymm4,ymm4,ymm6
1120: c4 c1 7d f9 f7 vpsubw ymm6,ymm0,ymm15
1125: c4 e2 7d 3a c6 vpminuw ymm0,ymm0,ymm6
112a: c5 fd 7f 04 24 vmovdqa YMMWORD PTR [rsp],ymm0
112f: c5 fd 6f 44 24 40 vmovdqa ymm0,YMMWORD PTR [rsp+0x40]
1135: c5 b5 e4 f0 vpmulhuw ymm6,ymm9,ymm0
1139: c5 b5 d5 c0 vpmullw ymm0,ymm9,ymm0
113d: c4 c1 7d d5 c6 vpmullw ymm0,ymm0,ymm14
1142: c4 c1 7d e4 c7 vpmulhuw ymm0,ymm0,ymm15
1147: c5 cd f9 f0 vpsubw ymm6,ymm6,ymm0
114b: c4 c1 4d fd c7 vpaddw ymm0,ymm6,ymm15
1150: c4 e2 4d 3a f0 vpminuw ymm6,ymm6,ymm0
1155: c5 f5 f9 c6 vpsubw ymm0,ymm1,ymm6
1159: c5 f5 fd ce vpaddw ymm1,ymm1,ymm6
115d: c4 c1 7d fd f7 vpaddw ymm6,ymm0,ymm15
1162: c4 e2 4d 3a f0 vpminuw ymm6,ymm6,ymm0
1167: c4 c1 75 f9 c7 vpsubw ymm0,ymm1,ymm15
116c: c4 e2 75 3a c8 vpminuw ymm1,ymm1,ymm0
1171: c4 c1 35 e4 c2 vpmulhuw ymm0,ymm9,ymm10
1176: c4 41 35 d5 d2 vpmullw ymm10,ymm9,ymm10
117b: c4 41 2d d5 d6 vpmullw ymm10,ymm10,ymm14
1180: c4 41 2d e4 d7 vpmulhuw ymm10,ymm10,ymm15
1185: c4 c1 7d f9 c2 vpsubw ymm0,ymm0,ymm10
118a: c4 41 7d fd d7 vpaddw ymm10,ymm0,ymm15
118f: c4 c2 7d 3a c2 vpminuw ymm0,ymm0,ymm10
1194: c5 6d f9 d0 vpsubw ymm10,ymm2,ymm0
1198: c5 ed fd d0 vpaddw ymm2,ymm2,ymm0
119c: c4 c1 2d fd c7 vpaddw ymm0,ymm10,ymm15
11a1: c4 c2 7d 3a c2 vpminuw ymm0,ymm0,ymm10
11a6: c4 41 6d f9 d7 vpsubw ymm10,ymm2,ymm15
11ab: c4 c2 6d 3a d2 vpminuw ymm2,ymm2,ymm10
// ...
However, there are some hints. For one, the symbols in the shared library tell you what kind of algorithm it is:
$ nm -D compute.so
0000000000002913 T inv_ntt
0000000000004748 T mul
0000000000001020 T ntt
It should then take at most some reading around to learn that NTT‑based polynomial multiplication means computing \[ f\cdot g = \mathrm{NTT}^{-1}\big(\mathrm{NTT}(f) \odot \mathrm{NTT}(g)\big) \,\text, \] where $\odot$ is coefficient‑wise multiplication. (This is an instance of the much more general theme that Fourier transforms turn convolutions into pointwise products. For beginners, I can recommend this 3Blue1Brown video on the topic.)
Among the three functions in the library,
it is to be expected that mul()
would be the easiest to understand:
Besides calls to NTT and inverse NTT,
it only contains the pointwise multiplications.
By staring at the code, one should be able to
deduce that a single multiplication looks like this:
; pointwise multiplication ymm2 = ymm0 * ymm1
vpmulhuw ymm2, ymm0, ymm1
vpmullw ymm1, ymm0, ymm1
vpmullw ymm1, ymm1, ymm14
vpmulhuw ymm1, ymm1, ymm15
vpsubw ymm2, ymm2, ymm1
vpaddw ymm1, ymm2, ymm15
vpminuw ymm2, ymm2, ymm1
The abundance of w suffixes
in the code strongly suggests that
the polynomial coefficients are packed
into the ymm vector registers
as 2‑byte integers.
Moreover, we see that
ymm15 and ymm14
are initialized with the constants
\[
\mathtt{ymm15} = \mathtt{0x2e01} = 11777 = q
\\
\mathtt{ymm14} = \mathtt{0xd201} = -11775 = 2-q
\]
at the beginning of the function.
From the absence of explicit modular arithmetic
and the presence of the constant $2-q = q^{-1}\bmod {2^{16}}$,
connoisseurs may recognize this piece of code as a
Montgomery multiplication:
It computes the low and high halves of the product,
finds a multiple of $q$ to subtract from the product
so that the low half becomes zero,
and returns the high half of the result,
thus effectively computing
$x{\cdot}y/2^{16}\bmod q$.
(Montgomery arithmetic is generally a common choice in vectorized code,
since typical vector instruction sets do not feature divisions with remainder.)
Having understood this, one should probably attempt to (perhaps just mentally) replace all occurrences of this multiplication routine in the code with a macro of some sort, in order to make it easier to focus on the higher-level structure of the computation. However, attempting to do so reveals that the inverse NTT uses a different multiplication algorithm! One way to recognize this is just from the constants that are being loaded in the beginning:
$ objdump -sd compute.so | grep -A200 '<[^@]*>:' | grep '>:\|mov.*eax'
0000000000001020 <ntt>:
102f: b8 01 2e 00 00 mov eax,0x2e01
103e: b8 01 d2 00 00 mov eax,0xd201
0000000000002913 <inv_ntt>:
2922: b8 01 2e 00 00 mov eax,0x2e01
2931: b8 ff 2d 00 00 mov eax,0x2dff
0000000000004748 <mul>:
4949: b8 01 2e 00 00 mov eax,0x2e01
4958: b8 01 d2 00 00 mov eax,0xd201
Notably, $\mathtt{0x2dff}$ is $q-2$ rather than $2-q$, suggesting that perhaps some part of the Montgomery multiplication happens with negated signs. Identifying and comparing the relevant code sequence appearing in the inverse NTT with the previously found multiplication routine confirms this:
ntt() and mul()
| inv_ntt()
|
|---|---|
|
|
ymm14
have subtractions in place of additions and vice versa.
However, this variant of Montgomery multiplication has a little
problem: When adding some multiple of $q$ that clears
the low half, there is almost always a carry into the high half.
Noticing that ymm13
holds the constant
$\mathtt{0xffff}=-1$
in inv_ntt(),
this is what the new
vpsubw ymm1, ymm1, ymm13
instruction takes care of.
However, there is a single exceptional case
that does not require adding the carry:
When the low half is already zero.
In that case, the result of the Montgomery multiplication
will be off by one.
This is the source of the observed occasional failures
of the mul() function!
Leakage, after all
Now, the most likely reason for the low half of a product to be zero is when one of the multiplicands was already equal to zero. Thus, we get the following rule, which should hold with overwhelming probability for random inputs:
If the overall polynomial multiplication was computed correctly,
then
no multiplications by zero happened inside the inverse NTT.
It may seem daunting to learn anything useful from this, but as it turns out things are actually fairly simple. The first step of the inverse NTT is to take $128$ pairs of two coefficients $(v_i,v_j)$ and apply a Gentleman–Sande butterfly to each of them, which is the following linear map: [source]
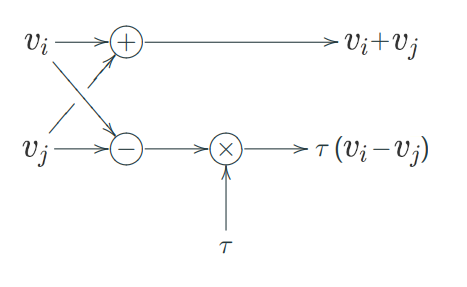
Here, $\tau$ is a nonzero constant that varies with the location $(i,j)$. This is exactly what we need: If $\tau(v_i-v_j)$ is computed correctly, then we learn that $v_i\neq v_j$. (Keep in mind that this operation happens — and hence, this observation holds true — for $128$ separate pairs of coefficients.)
Coming back to the bigger picture, recall that each of the coefficients $v_i$ entering the inverse NTT is itself a product of an unknown coefficient $\hat s_i$ of the NTT'd secret $\hat s$ with a coefficient $\hat c_i$ of the NTT'd ring element $\hat c$ contained in the ciphertext. Thus, the statement $v_i\neq v_j$ actually says $\hat s_i\hat c_i \neq \hat s_j\hat c_j$, and we can compute $\hat c_i$ and $\hat c_j$ by simply applying the NTT to $c$.
Turning such "disequations" into equations is conceptually easy: Just collect enough of them. With each query, we learn $\hat s_i\hat c_i \neq \hat s_j\hat c_j$, which is equivalent to $\hat s_j \neq \hat s_i\hat c_i/\hat c_j$ assuming $\hat c_j\neq0$. Since $\hat c_i,\hat c_j$ are random, we expect to observe all $q{\,-\,}1$ possible values $\hat c_i/\hat c_j$ eventually — the single exception is the impossible constant $\hat s_j/\hat s_i$, again assuming $\hat s_i\neq0$ for simplicity.
This gives rise to the following strategy for learning linear equations between the coefficients of the NTT'd secret $\hat s$: Query the server with a random, honestly generated ciphertext. Each time, for each of the $128$ pairs $(v_i,v_j)$ of coefficients entering a GS butterfly in the first layer of the inverse NTT, eliminate $\hat c_i/\hat c_j$ from the list of possible values of $\hat s_j/\hat s_i$. Repeat until there is only one possible ratio $\hat s_j/\hat s_i$ left for each of the $128$ pairs.
Lattices, after all
After some $250{,}000$ queries (which should take no more than a couple minutes when communication is properly pipelined — and yes, we did test this between two machines on opposite sides of the planet), we should have obtained exact linear equations between $128$ pairs of coefficients, effectively cutting the number of unknowns in half. Does this help? The previously employed dreamteam "lattice estimator + ChatGPT" is cautiously optimistic:


Here's the strategy for halving the dimension of the Ring‑LWE problem using the known linear relations: Write $\hat S\in \mathbb F_q^{128\times 256}$ for the matrix whose rows are a basis of the space of possible NTT'd secrets $\hat s$. Apply the inverse NTT to all rows (this can be written as a matrix product $\hat S\cdot M_\mathtt{INTT}$) to get a new matrix $S\in\mathbb F_q^{128\times 256}$. By construction, if $A$ is the matrix associated to the element $a\in R$ contained in the public key, the rows of $S\cdot A$ span a lattice of dimension $128$, embedded in $\mathbb Z^{256}$, that contains $s\cdot a\in R$.
At this point, we can basically chop off a bunch of redundant columns of everything and apply the uSVP attack (see for instance these nice slides) to an essentially half‑dimensional instance; see the code below for the hairy details. Solving the resulting lattice problem typically takes between 30 and 50 minutes on my laptop and seems to succeed much more often than not. (Almost all of the time is spent on BKZ‑reducing a $215$‑dimensional lattice with block size $45$.)
The flag, at last
pwn.py
#!/usr/bin/env python3
import socket, sys, random, hashlib, collections
from Crypto.Cipher import AES
n = 256
q = 11777
w = 8
################################################################
import ctypes, struct
lib = ctypes.CDLL('./compute.so')
pck = lambda v: struct.pack(f'@{n}H', *(c%q for c in v))
def wrap(lib_fun):
def fun(f):
lib_fun(buf := ctypes.create_string_buffer(pck(f), int(n*2)))
return list(struct.unpack(f'@{n}H', bytes(buf)))
return fun
ntt = wrap(lib.ntt)
################################################################
from vuln import sample, add, pck, unp, mul, center, extract, ppoly, pbits, hbits, mkaes, encaps, decaps
sub = lambda a,b: [(x-y)%q for x,y in zip(a,b)]
################################################################
sock = socket.socket()
sock.settimeout(5)
sock.connect((sys.argv[1], int(sys.argv[2])))
class ufail(Exception): pass
def get():
r = b''
while b'\n' not in r:
try: tmp = sock.recv(1)
except socket.error as e: tmp = b''
if not tmp: raise ufail(r)
r += tmp
return r.decode().strip()
pk_a = list(struct.unpack(f'<{n}H', bytes.fromhex(get().removeprefix('pk[0]: '))))
pk_b = list(struct.unpack(f'<{n}H', bytes.fromhex(get().removeprefix('pk[1]: '))))
pk = pk_a, pk_b
ct_c = list(struct.unpack(f'<{n}H', bytes.fromhex(get().removeprefix('ct[0]: '))))
ct_r = list(map('01'.index, get().removeprefix('ct[1]: ')))
ct_t = bytes.fromhex(get().removeprefix('ct[2]: '))
cipher = bytes.fromhex(get().removeprefix('flag: '))
ct = ct_c, ct_r, ct_t
def oracle(num=1):
sent = []
for _ in range(num):
bits,(c,r,t) = encaps(pk)
m1 = mkaes([1]+bits).encrypt(b'ping')
sock.sendall((struct.pack(f'<{n}H', *c).hex() + '\n').encode())
sock.sendall(''.join(map(str, r)).encode() + b'\n')
sock.sendall(t.hex().encode() + b'\n')
sock.sendall(m1.hex().encode() + b'\n')
sent.append((bits, (c,r,t)))
for bits,(c,r,t) in sent:
m2 = bytes.fromhex(get())
ok = mkaes([2]+bits).decrypt(m2) == b'pong'
yield ((c,r,t), ok)
################################################################
num_queries = 0
ratios = {i: set(range(q)) for i in range(n) if i%32<16}
while True:
for (c,r,t),ok in oracle(1000):
num_queries += 1
if not ok:
continue # bad sample, god knows what happened to it
cmid = ntt(c)
for i in ratios.keys():
j = i + 16
if not cmid[j]:
continue
# s[i]*c[i] - s[j]*c[j] != 0
# s[i]*c[i] != s[j]*c[j]
# s[j]/s[i] != c[i]/c[j]
ratio = cmid[i] * pow(cmid[j],-1,q) % q
ratios[i].discard(ratio)
print(f'{num_queries:7} {sum(len(r)>1 for r in ratios.values()):3}', [None if not r else list(r)[0] if len(r) == 1 else -len(r) for i,r in sorted(ratios.items())])
if all(len(r) <= 1 for r in ratios.values()):
break
fails = sum(not r for r in ratios.values())
if fails:
print(f'\x1b[33mfailed to leak {fails} equation{"s" if fails>1 else ""}\x1b[0m')
if fails > 3:
exit(1)
ratios = {i: list(rs)[0] for i,rs in ratios.items() if rs}
################################################################
shat_basis = []
for i,r in ratios.items():
v = [0]*n
v[i] = 1
v[i+16] = r
shat_basis.append(v)
for i in range(n):
if not any(v[i] for v in shat_basis):
v = [0]*n
v[i] = 1
shat_basis.append(v)
################################################################
from sage.all import *
load('solve.sage')
s = solve(pk_a, pk_b, shat_basis) # <-------
if s is None:
print(f'\x1b[1m!!\x1b[0m \x1b[31mno solution found!\x1b[0m')
exit(1)
print(f'\x1b[1m!!\x1b[0m \x1b[32m{s}\x1b[0m')
bits = decaps(s, pk, ct)
flag = mkaes([0]+bits).decrypt(cipher)
print()
print(f'--> \x1b[32m{flag}\x1b[0m')
print()
solve.sage
#!/usr/bin/env sage
proof.all(False)
n = 256
q = 11777
w = 8
################################################################
P.<T> = GF(q)[]
R.<t> = P.quotient(T^n + 1)
sample = lambda: [bin(getrandbits(w)).count('1') - w//2 for _ in range(n)]
add = lambda a,b: [c.lift_centered() for c in R(list(a))+R(list(b))]
sub = lambda a,b: [c.lift_centered() for c in R(list(a))-R(list(b))]
mul = lambda a,b: [c.lift_centered() for c in R(list(a))*R(list(b))]
################################################################
import ctypes, struct
lib = ctypes.CDLL('./compute.so')
pck = lambda v: struct.pack(f'@{n}H', *(c%q for c in v))
unp = lambda bs: struct.unpack(f'@{n}H', bytes(bs))
def wrap(lib_fun):
def fun(f):
lib_fun(buf := ctypes.create_string_buffer(pck(f), int(n*2)))
return list(struct.unpack(f'@{n}H', bytes(buf)))
return fun
ntt = wrap(lib.ntt)
nttmat = matrix(GF(q), [ntt(v) for v in (ZZ^n).gens()])
inttmat = ~nttmat
lift = lambda vec: vector(ZZ, (GF(q)(c).lift_centered() for c in list(vec)))
################################################################
import time
def solve(a, b, shatbas):
amat = matrix(ZZ, [mul(a, list((GF(q)^n).gens()[i])) for i in range(n)])
assert (lambda r: vector(GF(q), r) * amat == vector(GF(q), mul(a,r)))([randrange(q) for _ in range(n)])
shatlat = matrix(GF(q), shatbas)
slat = shatlat * inttmat
#-------------------------------
slatr = slat[:, :1]
amatr = amat[:, :amat.ncols()*5//6]
embw = 1
#-------------------------------
modqpart = slatr.augment(-slat*amatr)
ech = modqpart.echelon_form()
assert ech[:,:ech.nrows()] == 1
trafo = modqpart.solve_left(ech)
wdth = slatr.ncols() + amatr.ncols()
hght = slatr.nrows()
assert wdth >= hght
modq = matrix(wdth-hght, hght).augment(q * identity_matrix(wdth-hght))
modql, modqr = modq[:,:slatr.ncols()], modq[:,slatr.ncols():]
lat0 = block_matrix(ZZ, [
[ trafo*slatr, trafo*(-slat*amatr), matrix(slat.nrows(),1), ],
[ matrix(1,slatr.ncols()), matrix(b[:amatr.ncols()]), matrix([[embw]]), ],
[ modql, modqr, matrix(modq.nrows(),1), ],
])
print('dim =', lat0.dimensions())
print('det =', lat0.det())
print('log(|det|) =', lat0.det().abs().log(2).n())
# print(lat0)
# root Hermite factor
rhf = lambda vec: ((vec.norm() / lat0.det().abs()**(1/lat0.ncols()))**(1/lat0.ncols())).n()
t0 = time.time()
lat = matrix(filter(bool, lat0.LLL()))
print(time.time() - t0, '\x1b[35mLLL done\x1b[0m')
print('dim =', lat.dimensions())
# print(lat)
for beta in [45]:
t0 = time.time()
lat = lat.BKZ(block_size=beta, fp='rr', precision=200)
print(time.time() - t0, f'\x1b[35mBKZ-{beta} done\x1b[0m')
for vec in lat.rows():
if vec[-1] < 0:
vec = -vec
print(f'rhf:{rhf(vec)} nrm:{vec.norm().n()} {vec}')
if rhf(vec) < 1:
print(f'\x1b[36mrhf:{rhf(vec)} {vec.norm().n()} {vec}\x1b[0m')
comb = lat0.change_ring(GF(q)).solve_left(vec)
print(f'\x1b[1m??\x1b[21m \x1b[34m{comb}\x1b[0m')
assert comb[:slat.nrows()+1] * lat0[:slat.nrows()+1,:] == vec
s = lift(comb[:slat.nrows()] * trafo * slat)
print(f'\x1b[1m??\x1b[21m \x1b[33m{s}\x1b[0m')
if lift(sub(mul(s, a), b)).norm()^2 < (w+1)//2 * n:
print(f'\x1b[32mrhf:{rhf(vec)} {vec.norm().n()} {vec}\x1b[0m')
return list(s)
Output
$ time ./pwn.py 167.235.158.19 4422
1000 128 [-11124, -11124, -11117, -11118, -11125, -11123, -11121, -11119, -11120, -11116, -11118, -11122, -11131, -11129, -11123, -11131, -11123, -11126, -11123, -11114, -11125, -11118, -11121, -11117, -11116, -11118, -11119, -11128, -11116, -11115, -11119, -11118, -11124, -11118, -11115, -11125, -11120, -11121, -11125, -11116, -11119, -11114, -11121, -11118, -11120, -11127, -11123, -11116, -11119, -11116, -11115, -11125, -11119, -11125, -11123, -11118, -11126, -11125, -11122, -11112, -11119, -11120, -11114, -11119, -11125, -11119, -11123, -11120, -11122, -11124, -11118, -11124, -11126, -11117, -11119, -11120, -11121, -11114, -11120, -11123, -11115, -11127, -11133, -11117, -11116, -11123, -11130, -11119, -11120, -11120, -11122, -11126, -11119, -11122, -11123, -11116, -11126, -11128, -11119, -11120, -11121, -11122, -11115, -11120, -11127, -11121, -11110, -11125, -11121, -11121, -11121, -11119, -11120, -11118, -11117, -11117, -11123, -11120, -11120, -11121, -11119, -11117, -11119, -11123, -11120, -11120, -11117, -11121]
2000 128 [-10528, -10525, -10520, -10517, -10519, -10526, -10516, -10515, -10520, -10510, -10521, -10512, -10530, -10533, -10525, -10525, -10512, -10530, -10514, -10514, -10519, -10523, -10518, -10529, -10508, -10518, -10515, -10519, -10511, -10508, -10517, -10511, -10527, -10509, -10513, -10521, -10525, -10511, -10515, -10520, -10522, -10500, -10536, -10521, -10535, -10518, -10518, -10517, -10516, -10505, -10506, -10527, -10517, -10514, -10542, -10510, -10525, -10518, -10502, -10512, -10515, -10516, -10514, -10520, -10525, -10517, -10514, -10537, -10516, -10532, -10514, -10524, -10520, -10521, -10520, -10520, -10526, -10516, -10523, -10524, -10502, -10525, -10536, -10526, -10514, -10527, -10531, -10503, -10522, -10520, -10525, -10516, -10522, -10516, -10515, -10523, -10526, -10522, -10514, -10514, -10524, -10508, -10505, -10522, -10515, -10526, -10508, -10517, -10513, -10527, -10524, -10513, -10513, -10517, -10509, -10507, -10526, -10516, -10516, -10518, -10515, -10508, -10524, -10511, -10520, -10518, -10520, -10528]
3000 128 [-9953, -9942, -9938, -9919, -9925, -9949, -9945, -9924, -9936, -9924, -9937, -9923, -9960, -9947, -9924, -9924, -9932, -9941, -9929, -9927, -9920, -9944, -9941, -9954, -9928, -9936, -9947, -9934, -9927, -9924, -9948, -9931, -9956, -9936, -9921, -9935, -9946, -9923, -9938, -9923, -9945, -9921, -9956, -9924, -9948, -9940, -9941, -9937, -9936, -9928, -9913, -9944, -9921, -9931, -9939, -9911, -9943, -9931, -9906, -9918, -9928, -9941, -9921, -9939, -9943, -9952, -9924, -9946, -9925, -9948, -9939, -9938, -9927, -9938, -9938, -9946, -9932, -9938, -9945, -9941, -9927, -9925, -9942, -9943, -9932, -9933, -9936, -9933, -9942, -9932, -9932, -9930, -9944, -9937, -9930, -9951, -9947, -9925, -9928, -9918, -9944, -9932, -9935, -9934, -9944, -9960, -9923, -9925, -9941, -9938, -9929, -9939, -9932, -9937, -9928, -9938, -9933, -9943, -9932, -9933, -9929, -9925, -9934, -9919, -9938, -9937, -9939, -9961]
// ...
260000 1 [5320, 10257, 4096, 6890, 9083, 7912, 10732, 2864, 1845, 9883, 9538, 7131, 8788, 11690, 1074, 9894, 8892, 2120, 2385, 3126, 9852, 8389, 3392, 3789, 8012, 4327, 9191, 5249, 716, 4321, 10155, 6309, 6429, 9346, 1256, 5844, 3456, 11467, 1310, 10726, 6644, 3638, 6206, 2032, 10754, 8362, 8807, 5338, 2979, 1526, 5609, 5391, 9269, 9237, 8177, 777, 9645, 10453, 9839, 11054, 8295, 11635, 3314, 9639, 3530, 2156, 3835, 8398, 1280, 9238, 10248, 7273, 5322, 7510, 6809, 1129, 6276, 2100, 6914, 9238, 6443, 2177, 7440, 3198, 1797, 9167, 10563, 387, 463, 3009, 5627, 9985, 4899, 9838, 7498, 48, 4348, 9644, -2, 9673, 11307, 8737, 7841, 9038, 163, 11256, 6525, 2805, 4659, 3456, 10488, 8221, 5658, 784, 552, 9743, 11439, 6535, 9693, 9163, 778, 5012, 9810, 11039, 3404, 4454, 3257, 3897]
261000 1 [5320, 10257, 4096, 6890, 9083, 7912, 10732, 2864, 1845, 9883, 9538, 7131, 8788, 11690, 1074, 9894, 8892, 2120, 2385, 3126, 9852, 8389, 3392, 3789, 8012, 4327, 9191, 5249, 716, 4321, 10155, 6309, 6429, 9346, 1256, 5844, 3456, 11467, 1310, 10726, 6644, 3638, 6206, 2032, 10754, 8362, 8807, 5338, 2979, 1526, 5609, 5391, 9269, 9237, 8177, 777, 9645, 10453, 9839, 11054, 8295, 11635, 3314, 9639, 3530, 2156, 3835, 8398, 1280, 9238, 10248, 7273, 5322, 7510, 6809, 1129, 6276, 2100, 6914, 9238, 6443, 2177, 7440, 3198, 1797, 9167, 10563, 387, 463, 3009, 5627, 9985, 4899, 9838, 7498, 48, 4348, 9644, -2, 9673, 11307, 8737, 7841, 9038, 163, 11256, 6525, 2805, 4659, 3456, 10488, 8221, 5658, 784, 552, 9743, 11439, 6535, 9693, 9163, 778, 5012, 9810, 11039, 3404, 4454, 3257, 3897]
262000 1 [5320, 10257, 4096, 6890, 9083, 7912, 10732, 2864, 1845, 9883, 9538, 7131, 8788, 11690, 1074, 9894, 8892, 2120, 2385, 3126, 9852, 8389, 3392, 3789, 8012, 4327, 9191, 5249, 716, 4321, 10155, 6309, 6429, 9346, 1256, 5844, 3456, 11467, 1310, 10726, 6644, 3638, 6206, 2032, 10754, 8362, 8807, 5338, 2979, 1526, 5609, 5391, 9269, 9237, 8177, 777, 9645, 10453, 9839, 11054, 8295, 11635, 3314, 9639, 3530, 2156, 3835, 8398, 1280, 9238, 10248, 7273, 5322, 7510, 6809, 1129, 6276, 2100, 6914, 9238, 6443, 2177, 7440, 3198, 1797, 9167, 10563, 387, 463, 3009, 5627, 9985, 4899, 9838, 7498, 48, 4348, 9644, -2, 9673, 11307, 8737, 7841, 9038, 163, 11256, 6525, 2805, 4659, 3456, 10488, 8221, 5658, 784, 552, 9743, 11439, 6535, 9693, 9163, 778, 5012, 9810, 11039, 3404, 4454, 3257, 3897]
263000 0 [5320, 10257, 4096, 6890, 9083, 7912, 10732, 2864, 1845, 9883, 9538, 7131, 8788, 11690, 1074, 9894, 8892, 2120, 2385, 3126, 9852, 8389, 3392, 3789, 8012, 4327, 9191, 5249, 716, 4321, 10155, 6309, 6429, 9346, 1256, 5844, 3456, 11467, 1310, 10726, 6644, 3638, 6206, 2032, 10754, 8362, 8807, 5338, 2979, 1526, 5609, 5391, 9269, 9237, 8177, 777, 9645, 10453, 9839, 11054, 8295, 11635, 3314, 9639, 3530, 2156, 3835, 8398, 1280, 9238, 10248, 7273, 5322, 7510, 6809, 1129, 6276, 2100, 6914, 9238, 6443, 2177, 7440, 3198, 1797, 9167, 10563, 387, 463, 3009, 5627, 9985, 4899, 9838, 7498, 48, 4348, 9644, 10722, 9673, 11307, 8737, 7841, 9038, 163, 11256, 6525, 2805, 4659, 3456, 10488, 8221, 5658, 784, 552, 9743, 11439, 6535, 9693, 9163, 778, 5012, 9810, 11039, 3404, 4454, 3257, 3897]
dim = (215, 215)
det = 128523355212312984740482083941262861951183664818213117392658355763911676483262820940871293704572209997969344568368573664129974370880969790012879529100120020972774362199763666440288493137415545233266753570155201424002582071152741974278571893757836092110540902092387401351720488413371942895068455348678668372414388266339767150349996223748142190450930689
log(|det|) = 1163.03686375978
16.31879711151123 LLL done
dim = (215, 215)
1571.3907492160797 BKZ-45 done
rhf:0.996645908137457 nrm:20.6397674405503 (0, 0, 0, -1, -1, -2, 0, -1, -1, -4, 0, 2, 1, 0, -1, 2, 0, -1, -2, 1, 2, 0, 0, -1, 0, -2, -1, 0, 3, 2, -1, 4, -1, 1, 2, 3, -2, -1, 1, 0, -1, 0, 1, 0, 1, 0, 0, -3, -1, -1, 2, 2, -1, 2, 0, 0, 1, 0, 0, 0, -2, -2, -3, 0, 0, 1, 0, 1, -1, 1, -1, 1, -1, 0, 1, -1, 1, 2, 2, 0, -2, -1, -2, 0, -1, 0, -2, 0, 0, -1, 1, 1, -3, 2, 0, 1, -1, 0, 0, -1, -2, 0, 1, 1, 3, -1, 0, -1, -2, -1, -1, -2, -1, 1, -1, 0, -1, 1, -1, 0, 0, 1, 1, 1, -1, 0, 1, -2, -3, -1, 0, 2, 0, 3, -2, 1, -2, -2, -1, 1, 0, -1, 0, -3, 1, -3, 0, 0, 3, -2, -3, 2, -1, -1, -2, 0, 1, 1, 0, -1, -1, 2, -2, -2, -2, 2, -1, -3, -1, 0, 0, -1, 0, 2, 1, 2, 2, -1, -3, 1, -2, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, -1, 1, 0, -1, -1, 1, 0, 1, 2, 1, 0, 1, 0, 0, 2, -2, 0, -2, -1, -1, 0, 0, -2, 1)
rhf:0.996645908137457 20.6397674405503 (0, 0, 0, -1, -1, -2, 0, -1, -1, -4, 0, 2, 1, 0, -1, 2, 0, -1, -2, 1, 2, 0, 0, -1, 0, -2, -1, 0, 3, 2, -1, 4, -1, 1, 2, 3, -2, -1, 1, 0, -1, 0, 1, 0, 1, 0, 0, -3, -1, -1, 2, 2, -1, 2, 0, 0, 1, 0, 0, 0, -2, -2, -3, 0, 0, 1, 0, 1, -1, 1, -1, 1, -1, 0, 1, -1, 1, 2, 2, 0, -2, -1, -2, 0, -1, 0, -2, 0, 0, -1, 1, 1, -3, 2, 0, 1, -1, 0, 0, -1, -2, 0, 1, 1, 3, -1, 0, -1, -2, -1, -1, -2, -1, 1, -1, 0, -1, 1, -1, 0, 0, 1, 1, 1, -1, 0, 1, -2, -3, -1, 0, 2, 0, 3, -2, 1, -2, -2, -1, 1, 0, -1, 0, -3, 1, -3, 0, 0, 3, -2, -3, 2, -1, -1, -2, 0, 1, 1, 0, -1, -1, 2, -2, -2, -2, 2, -1, -3, -1, 0, 0, -1, 0, 2, 1, 2, 2, -1, -3, 1, -2, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, -1, 1, 0, -1, -1, 1, 0, 1, 2, 1, 0, 1, 0, 0, 2, -2, 0, -2, -1, -1, 0, 0, -2, 1)
?? (0, 10281, 9815, 3519, 4588, 1719, 2586, 2236, 1782, 2232, 1760, 9808, 8285, 1496, 2514, 752, 4650, 6841, 6267, 5090, 10482, 5714, 4721, 10948, 6712, 5131, 7847, 595, 2245, 1016, 7147, 4556, 1232, 9319, 388, 9170, 6109, 6141, 8242, 8524, 4833, 10737, 3725, 2541, 10949, 1056, 5449, 5940, 3044, 8543, 9710, 7453, 4517, 194, 2306, 3911, 6029, 10337, 283, 6096, 1533, 765, 6818, 7329, 6384, 6570, 2142, 9103, 1582, 7978, 9926, 6336, 645, 2230, 7923, 7758, 640, 1490, 11003, 7084, 9732, 4982, 11765, 2734, 1553, 4631, 991, 6472, 659, 10225, 7292, 10374, 7176, 9077, 2177, 6415, 11148, 6727, 9782, 11497, 9743, 9991, 810, 6403, 5250, 10224, 636, 6859, 4703, 11251, 5131, 5751, 8924, 10747, 6864, 2359, 10324, 1147, 4930, 10079, 6052, 2180, 4890, 1747, 9678, 1355, 4036, 6942, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
?? (0, 0, -2, 2, 0, 1, 0, 0, 1, 2, -1, 2, 2, -2, 0, 0, 1, 0, -2, 0, 1, 1, -1, 3, 0, 2, 0, 2, -3, 2, 2, 1, 2, 0, -1, -2, 1, 2, 1, 1, 1, 2, -1, 1, -2, 1, 1, -1, 2, 2, 1, 0, -2, -1, 1, 1, -1, 0, -1, 1, 0, -1, 0, 1, 0, 0, 1, -1, 0, -3, 0, -2, 1, 3, -1, -1, 0, -1, 1, 1, -2, 0, 2, 3, 1, -1, 1, -1, -1, 0, 1, -1, 1, -2, -1, 0, 0, 0, 0, -2, 2, -1, -1, 0, 0, 0, 1, -1, -2, 0, 0, 0, 1, 0, 1, 0, 0, -2, 0, -4, -1, 1, 0, -1, -3, 1, 0, 4, 1, 0, 1, -1, 1, -3, -3, 1, 2, -2, 0, -1, -1, -2, 2, -1, -1, 1, -1, 2, 1, -2, 1, -2, 0, 2, -1, -1, 1, 1, -1, 0, 2, 0, 0, 1, -1, 1, 1, -1, -1, 0, -2, 1, -1, -1, -2, -1, 0, -1, 2, 1, -1, 2, 1, 0, 1, 1, 0, 1, -2, 0, -1, 1, 0, 0, -3, 0, -3, -1, -1, -2, 0, -1, 0, -1, 1, -1, -1, 1, 0, -3, 0, 1, -1, 0, 1, 1, -1, -3, -1, 1, 1, 0, 0, -2, -1, 1, 0, 1, -1, 0, 0, 0, -1, 0, 0, 1, -2, -1, 0, 1, -1, 0, 0, -2, -3, 1, -1, -1, 1, 2, -2, -2, 0, 0, 1, 0)
rhf:0.996645908137457 20.6397674405503 (0, 0, 0, -1, -1, -2, 0, -1, -1, -4, 0, 2, 1, 0, -1, 2, 0, -1, -2, 1, 2, 0, 0, -1, 0, -2, -1, 0, 3, 2, -1, 4, -1, 1, 2, 3, -2, -1, 1, 0, -1, 0, 1, 0, 1, 0, 0, -3, -1, -1, 2, 2, -1, 2, 0, 0, 1, 0, 0, 0, -2, -2, -3, 0, 0, 1, 0, 1, -1, 1, -1, 1, -1, 0, 1, -1, 1, 2, 2, 0, -2, -1, -2, 0, -1, 0, -2, 0, 0, -1, 1, 1, -3, 2, 0, 1, -1, 0, 0, -1, -2, 0, 1, 1, 3, -1, 0, -1, -2, -1, -1, -2, -1, 1, -1, 0, -1, 1, -1, 0, 0, 1, 1, 1, -1, 0, 1, -2, -3, -1, 0, 2, 0, 3, -2, 1, -2, -2, -1, 1, 0, -1, 0, -3, 1, -3, 0, 0, 3, -2, -3, 2, -1, -1, -2, 0, 1, 1, 0, -1, -1, 2, -2, -2, -2, 2, -1, -3, -1, 0, 0, -1, 0, 2, 1, 2, 2, -1, -3, 1, -2, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, -1, 1, 0, -1, -1, 1, 0, 1, 2, 1, 0, 1, 0, 0, 2, -2, 0, -2, -1, -1, 0, 0, -2, 1)
!! [0, 0, -2, 2, 0, 1, 0, 0, 1, 2, -1, 2, 2, -2, 0, 0, 1, 0, -2, 0, 1, 1, -1, 3, 0, 2, 0, 2, -3, 2, 2, 1, 2, 0, -1, -2, 1, 2, 1, 1, 1, 2, -1, 1, -2, 1, 1, -1, 2, 2, 1, 0, -2, -1, 1, 1, -1, 0, -1, 1, 0, -1, 0, 1, 0, 0, 1, -1, 0, -3, 0, -2, 1, 3, -1, -1, 0, -1, 1, 1, -2, 0, 2, 3, 1, -1, 1, -1, -1, 0, 1, -1, 1, -2, -1, 0, 0, 0, 0, -2, 2, -1, -1, 0, 0, 0, 1, -1, -2, 0, 0, 0, 1, 0, 1, 0, 0, -2, 0, -4, -1, 1, 0, -1, -3, 1, 0, 4, 1, 0, 1, -1, 1, -3, -3, 1, 2, -2, 0, -1, -1, -2, 2, -1, -1, 1, -1, 2, 1, -2, 1, -2, 0, 2, -1, -1, 1, 1, -1, 0, 2, 0, 0, 1, -1, 1, 1, -1, -1, 0, -2, 1, -1, -1, -2, -1, 0, -1, 2, 1, -1, 2, 1, 0, 1, 1, 0, 1, -2, 0, -1, 1, 0, 0, -3, 0, -3, -1, -1, -2, 0, -1, 0, -1, 1, -1, -1, 1, 0, -3, 0, 1, -1, 0, 1, 1, -1, -3, -1, 1, 1, 0, 0, -2, -1, 1, 0, 1, -1, 0, 0, 0, -1, 0, 0, 1, -2, -1, 0, 1, -1, 0, 0, -2, -3, 1, -1, -1, 1, 2, -2, -2, 0, 0, 1, 0]
--> b'hxp{iF_y0u_g4z3_l0Ng_1Nt0_a_L4tT1c3__Th3_l4Tt1c3_g4z3S_b4Ck_4t_Y0u}'
real 29m2.043s
user 29m1.685s
sys 0m2.114s
